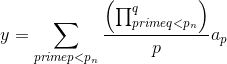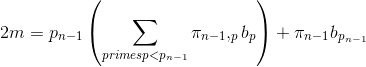Prime number formula

Consider an integer y = 3a2 + 2a3, where a2 is any integer, positive or negative, which is not divisible by 2, and likewise, a3 is an integer not divisible by 3. It's pretty straight forward to show that y is not divisible by 2 or 3.

We can continue with this logic to find a formula for an integer which is not divisible by 2, 3 or 5. The formula is y = 3·5a2 + 2·5a3 + 2·3a5, where a2, a3 and a5 are not divisible by 2, 3 or 5, respectively.

More generally, we can devise a formula to find all prime numbers in an interval [pn, pn2], where pn is the nth prime number, if we know all the primes p1 to pn-1. The equation in all it's glory is:



Where ap is any number not divisible by p.

So it's pretty simple, and while it might make it slightly easier to compute primes, the task still requires all the same information as it did before. There are a few questions that remain however:

1) Will all primes have a solution to this equation? I think it's possible to show this by showing that if we replace all the ap's with bp's, where the bp's can be any integers, then any integer y has a solution to the equation.

2) Given an integer, is it possibly to use the equation to determine if it's prime? I think this is actually fairly straight forward. The problem is that it doesn't seem to me like it would be computationally faster than existing methods.

3) Can we use this equation to determine the number of primes in an interval [pn, pn2]? If the solutions can be ordered in a nice way, then I think the answer is yes, otherwise, I think the problem would resemble the Sieve of Eratosthenes in some way.

There are a set of 4 prime number problems known as Landau's problems. I think this formula might be useful for solving some of these. I've already had a go at Goldbach's conjecture and I'm satisfied that the conjecture's true, although I haven't proved it. I'll post what I've got later.

I probably should have mentioned that the reason the equation only gives primes in the interval [pn, pn2] is because every integer below pn2 is either divisible by one of p1, p2, ... , pn-1 or is prime. So the formula will continue to give primes up to infinity, but it will also give composite numbers with prime factors of pn or higher. All the primes below the interval are multiples of themselves, which means the equation shouldn't give these primes at all, except for 1.

Another thing we can do is take the last term of the summation out of the equation, and factor out pn-1 to get a recursive formula for prime numbers:



Where k is a number which is not divisible by p1, p2, ... , pn-2.

So for the equation y = 3·5a2 + 2·5a3 + 2·3a5 we get:

y = 5(3a2 + 2a3) + 2·3a5

But 3a2 + 2a3 is just a number which is not divisible by 2 or 3, let's call it k, so:

y = 5k + 2·3a5

For the general equation we might as well just let k be a prime in the interval [pn-1, pn-12] for aesthetic purposes, although it doesn't need to be.

James McCanney has found the solution to this age old problem and has written a book describing how to calculate primes in a simple way. The book "Calculate Primes - Direct propagation of the Prime Numbers" can be purchased at his website: http://www.jmccanneyscience.com/SecWebOrderPg.htm Price of the book is $29.90 including shipping to any of the 50 US States. The description of the book is found here:
http://www.jmccanneyscience.com/CalculatePrimesCoversandTableofContents.HTM
Hope this helps you.

I was also curious about McCanney's book, but judging by this thread it'll also be over my head.

One way to test your equation would be to make it into a program. Does it require iteration or is it done with one calculation?

Also, can you show it in action doing it by hand?

Richard S said:

James McCanney has found the solution to this age old problem and has written a book describing how to calculate primes in a simple way. The book "Calculate Primes - Direct propagation of the Prime Numbers" can be purchased at his website: http://www.jmccanneyscience.com/SecWebOrderPg.htm Price of the book is $29.90 including shipping to any of the 50 US States. The description of the book is found here:
http://www.jmccanneyscience.com/CalculatePrimesCoversandTableofContents.HTM
Hope this helps you.

Click to expand...

monotonic said:

I was also curious about McCanney's book, but judging by this thread it'll also be over my head.

One way to test your equation would be to make it into a program. Does it require iteration or is it done with one calculation?

Also, can you show it in action doing it by hand?

Click to expand...

I don't think I'll read the book either, I've already got lots of stuff to read. But does anyone know what his formula is? I'd be interested to know.

If we just look at the equation y = 3a2 + 2a3 and just set a2 = 1, then we get y = 3 + 2a3 where a3 is any number not divisible by 3, so: 1, 2, 4, 5, 7, 8 etc. This means that y is: 5, 7, 11, 13, 17, 19. Essentially all it's doing is skipping every even number, and then skipping every even number which is a multiple of 3. This will give all the primes between 5 and 25 because every number less than 25 is either a multiple of 2 and/or 3, or is prime.

If we now take a look at the equation y = 3·5a2 + 2·5a3 + 2·3a5 which is y = 15a2 + 10a3 + 6a5 and set a2 = 1 and a3 =1 then y 15 + 10 + 6a5, where a5 is any number which is not divisible by 5, i.e. 1, 2, 3, 4, 6, 7, 8, 9. This gives y as 31, 37, 43, 49, 61, 67, 73, 79. 49 isn't a prime but it's 72, so it's not a multiple of 2, 3, or 5, and is outside of the interval. If we set a2 = 1 and a3 = 2 then y = 15 + 20 + 6a5 so y is: 41, 47, 53, 59, 71, 77, 83, 89. 77 isn't a prime either but it's 7 x 11, so isn't a multiple of 2, 3 or 5, and is outside the interval as well.

Archaea said:

I've already had a go at Goldbach's conjecture and I'm satisfied that the conjecture's true, although I haven't proved it.

Click to expand...

Isn't the point of mathematics not to be satisfied that something is true until it is proven? On what mathematical grounds could you be satisfied that an unproven conjecture is true? This seems like the case of the English person who observed many swans in their country, all of them white, and came to the conclusion that "All swans are white", then they went to Australia and saw a black swan.

It is important not to pretend we have absolute knowledge, but at the same time we can't let the lack of absolute knowledge keep us from running with a given theory if we can, in order to increase our knowledge.

At any rate, Goldbach's conjecture is verified to 4x10^18, so even if it's not proven will it really matter unless you use larger numbers than that?

I think pure mathematics differs from the empirical sciences in that it does seek absolute knowledge within its sphere of activity.

It might not matter on a practical level if someone thought:

2 + 2 = 4.000000000000000001

but mathematically it wouldn't be true, given the shared starting assumptions about what the terms and functions signify. From the standards of mathematical proof, "almost proven" is "not proven at all".

A prime number is one that is only divisible into whole integers of 1 and itself. So 5 is a prime number because it is only divisible into 1 x 5 = 5. 6 is not a prime number because it is divisible into 2 x 3 = 6.

The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19 [. . .]

A conjecture could be made that if you multiply consecutive prime numbers together, and then add 1, then the result will also be a prime number.

For example:

2 x 3 +1 = 7 Seven is a prime number.

2 x 3 x 5 + 1 = 31 Thirty-one is a prime number.

2 x 3 x 5 x 7 + 1 = 211 Two-hundred and eleven is a prime number.

2 x 3 x 5 x 7 x 11 + 1 = 2311 Two-thousand three-hundred and eleven is a prime number.

At this point, a good number of people might be satisfied that the conjecture is true.

Unfortunately the next instance proves that the conjecture is not true:

2 x 3 x 5 x 7 x 11 x 13 + 1 = 30,031 Thirty-thousand and thirty-one is not a prime number, it is divisible by 59 and 509. 59 x 509 = 30,031

Mal7 said:

Archaea said:

I've already had a go at Goldbach's conjecture and I'm satisfied that the conjecture's true, although I haven't proved it.

Click to expand...

Isn't the point of mathematics not to be satisfied that something is true until it is proven? On what mathematical grounds could you be satisfied that an unproven conjecture is true? This seems like the case of the English person who observed many swans in their country, all of them white, and came to the conclusion that "All swans are white", then they went to Australia and saw a black swan.

Click to expand...

True, the reason I haven't posted what I've done with the Goldbach conjecture is that I'm still working on some of it, and I haven't proved it completely yet, but I really do think it must be true. I'm also pretty lazy and communicating is hard, but I'll just do it now. :)

First, though, I want to define:



And:



These will just make writing things out easier. So the prime number formula is:



And we can take the last term out of the summation and factor out pn-1 from what's left over to get:



For Goldbach's conjecture all that's needed is to add two prime numbers (y1 and y2) together:



Where ap and cp are any two integers which aren't divisible by p. The interesting thing is that when we add these two integers we can get any integer we like. Except for when p = 2, in which case a2 + c2 must be an even integer, this makes sense though because all other πn,p have factors of 2, so π2,p is the only odd πn,p.

All that we need to show now is that there is a solution to this equation for every integer m:



Where bp = ap + cp. I think this can be done by using the fact that pn-1 and πn-1 are co-prime. This would mean that for every even integer there are an infinite number of pairs of primes (where primes can be either positive or negative primes) which sum to the integer. All that would be left to show is that there exists a pair of positive primes which sum to the integer.

We can show that:



Can be satisfied for any m by using Mathematical induction

Basis step: All we need to do is show that there are solutions to the equation 2m = 3b2 + 2b3, where b2 = a2 + c2 and b3 = a3 + c3. b2 must be an even integer, so b2 = 2d, for any integer d, and b3 can be any integer at all.

Dividing by 2 gives:

m = 3d + b3

Which means that for any even number it's possible to find a pair of numbers which aren't divisible by 2 or 3 and add up to the even number.

Inductive step: Assume that for any even number (2e) there exists a pair of numbers k1 and k2 which aren't divisible by p1, p2, ... , pn-2 and add up to the even number. Now take the equation:



And take the last term out of the summation and factor out pn-1 from the remaining terms to get:



By reversing the logic in my previous post it should be possible to show that:

2m = pn-1(k1 + k2) + πn-1bp_n-1
2m = pn-1(2e) + (πn-1)bp_n-1

dividing by 2:

m = pn-1e + (πn-1/2)bp_n-1

Since pn-1 and πn-1/2 share no common prime factors they are Coprime integers. This means that there are integers f and g such that pn-1f + (πn-1/2)g = 1, this is a result called Bézout's identity. So just let e = mf and bp_n-1 = mg and the equation is satisfied.

This proves that there are infinite pairs of numbers (y1 and y2) which aren't divisible by p1, p2, .. , pn-1 and add up to any given even number. All that's left to show in order to prove the Goldbach conjecture is that one of these pairs will have both y1 and y2 in the interval [pn, pn2] thus making sure they're prime.


A quick example, let 2m = 38, and y1 + y2 = 15b2 + 10b3 + 6b5. b2 is an even integer, so let b2 = 2d, putting this all together:

38 = 15·2d + 10b3 + 6b5
19 = 15d + 5b3 + 3b5

One solution to this is d = 1, b3 = 2, b5 = -2. Splitting up the b's:

b2 = 2, so let a2 = 1 and c2 = 1 (both odd numbers)
b3 = 2, so let a3 = 1 and c3 = 1 (both not divisible by 3)
b5 = -2, so let a5 = -1 and c5 = -1 (both not divisible by 5)

Both prime numbers are:

15(1) + 10(1) + 6(-1) = 19

We can get two other numbers by letting:

a2 = 1 and c2 = 1
a3 = 4 and c3 = -2
a5 = -3 and c3 = 1

To get:

15(1) + 10(4) + 6(-3) = 37
15(1) + 10(-2) + 6(1) = 1

1 isn't in the interval [7, 49], and it's possible to get negative numbers as well.

I probably should have posted this before the stuff on the Goldbach conjecture. Going back to the first question in my original post:

1) Will all primes have a solution to this equation? I think it's possible to show this by showing that if we replace all the ap's with bp's, where the bp's can be any integers, then any integer y has a solution to the equation.

Click to expand...

If we can show that y can be any integer when the ap's no longer need to be integers not divisible by p (and hence become bp's) then it follows that the prime number formula will give all the primes greater than pn-1. We can do this by using mathematical induction again:

Basis step: All we need to show here is that for the equation y = 3b2 + 2b3, where b2 and b3 can be any integers, that there is a solution for every integer y. Since 2 and 3 are co-prime there exist integers f and g such that 3f + 2g = 1. So let b2 = yf and b3 = yg and the equation is satisfied.

Inductive step: It has previously been shown that:

y = pn-1k + πn-1bp_n-1

If we assume that k can be any integer, then since bp_n-1 can also be any integer, and again using the fact that pn-1 and πn-1 are co-prime, there is a solution for any integer y.

This means that when all the ap's are not divisible by p, y is not divisible by p1, p2, ... , pn-1, but if any of the ap's are divisible by p, then y has a prime factor of p.


It's also possible to use the Goldbach stuff from my previous post to prove the Twin prime conjecture. If we subtract y2 from y1 we get:

y1 - y2 = pn-1(k1 - k2) + πn-1Bp_n-1

Where Bp = ap - cp, and there will be solutions for ap and cp if Bp is any integer. It's possible to show that k1 - k2 can be any even integer using the same logic as in my previous post but with a minus sign instead of a plus sign and Bp's instead of bp's, so let k1 - k2 = 2e, and set y1 - y2 = 2, because they're twin primes. We now have:

2 = pn-1(2e) + πn-1Bp_n-1

And divide by 2:

1 = pn-1e + (πn-1/2)Bp_n-1

pn-1 and πn-1/2 are co-prime, so there is an e and Bp_n-1 which satisfies the equation. In fact there are infinite solutions to the equation Bp = ap - cp so there are infinite pairs of numbers not divisible by p1, p2, ... , pn-1 which are only separated by 2.

Since there are infinite pairs and infinite intervals, and any negative pair of twin primes correspond to a positive pair, I thought maybe that would prove the conjecture. But now I'm wondering whether it still needs to be shown that at least one of these pairs is in the interval.