G
Guest 15258
Guest
The latest session (Session 4 July 2020) contained this fun snippet,
This stuff relates to something I've been thinking about recently. Suppose the ether is made up of particles which are more "fundamental" than space. I.e. Space is an illusion created by the way these particles communicate with each other. The thinking is that these particles are ether particles and they communicate using light.
@John G these are like space vertices, communicating with each other like a cellular automata.
Now suppose that the number of particles which a single particle can communicate with directly is equal for all particles. Then if we map these particles into 3 dimensional space (R^3), such that "close" particles are close in 3D space under the map, then maybe if we draw in the edges (light paths), the edges pass through the vertices of a platonic solid whose center is at the particle.
I'm not explaining this very well. Here's a picture,
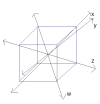
Here's 3rd density, The black lines are the axes of R^3, the red points are the images of the ether particles under the map to R^3, and the blue lines are the octahedron (which is a platonic solid) formed by particles closest to the particle in the center.
Here's another picture,
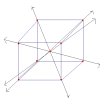
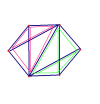
This is what I think 4th density might be like. There are 4 black axes, which give us something like 4 dimensional space (R^4), the red points are the ether particles and the blue lines form a cube (another platonic solid) of "close" particles. So the way light moves in 4th density gives space the structure of R^4 with some funny geometry.
So if this is right and a pentagon in 3rd density is a triangle in 4th density, then there must be some map which takes pentagons to triangles or something, I dunno. This is as far as I've gotten.
(Ark) Yes. Two questions. First question is goes back to December 1998. Twenty-two years ago, I was asking about gravity and Kaluza-Klein theory and multidimensional universes. I was told I was on the right track. I asked whether I missed something, and the answer was, "You did not miss anything. You have not yet found something." And then I asked what was it, and the answer was: tetrahedron. And it didn't fit any of my ideas. Tetrahedron is a geometric figure, a solid body in 3 dimensions. And I didn't ask then what the meaning of the tetrahedron was related to gravity. But now I really would like to know whether it is really a tetrahedron in our space, or a symbolic expression that there are four of something - but of what? Can I have some explanation after 22 years? I'm slow, yeah?
(Joe) Well, you waited long enough, so you should get an answer!
A: Tetrahedron in 3D is what in 4D?
Q: (Ark) Tetrahedron in 3D is what in 4D...
A: Lethbridge.
Q: (Pierre) Coral castle.
(Joe) No, pendulums.
(Ark) The magnetic something?
(Joe) He adjusted the length of pendulums to dowse into different dimensions.
(Andromeda) He was drawing pentagrams and they were triangles in another dimension.
(Gaby) I think it was pentagons that he drew in 3rd density, and that was triangles in 4th density.
A: Yes
Q: (Ark) What is this Lethbridge? It's a book that I should look at?
A: Yes
Q: (Joe) We have it. It's a short book.
(Ark) Alright, I will look and try to figure it out. Second question of a similar kind... It goes back to 24th of July 1999. I was again asking about theories of gravity and how to expand the theory of gravity because gravity is so important. Then, there was a unexpected combination of words which was, "octagonal complexigram". That was the answer. And I have no idea... I mean, complexigram, I have an idea. There are complex numbers, right? So complex numbers, it probably has to do with...
A: Double tetrahedron in 3D is hexagon in 4D.
Q: (Ark) But here it was octagonal, and not hexagonal.
This stuff relates to something I've been thinking about recently. Suppose the ether is made up of particles which are more "fundamental" than space. I.e. Space is an illusion created by the way these particles communicate with each other. The thinking is that these particles are ether particles and they communicate using light.
@John G these are like space vertices, communicating with each other like a cellular automata.
Now suppose that the number of particles which a single particle can communicate with directly is equal for all particles. Then if we map these particles into 3 dimensional space (R^3), such that "close" particles are close in 3D space under the map, then maybe if we draw in the edges (light paths), the edges pass through the vertices of a platonic solid whose center is at the particle.
I'm not explaining this very well. Here's a picture,

Here's 3rd density, The black lines are the axes of R^3, the red points are the images of the ether particles under the map to R^3, and the blue lines are the octahedron (which is a platonic solid) formed by particles closest to the particle in the center.
Here's another picture,

This is what I think 4th density might be like. There are 4 black axes, which give us something like 4 dimensional space (R^4), the red points are the ether particles and the blue lines form a cube (another platonic solid) of "close" particles. So the way light moves in 4th density gives space the structure of R^4 with some funny geometry.
So if this is right and a pentagon in 3rd density is a triangle in 4th density, then there must be some map which takes pentagons to triangles or something, I dunno. This is as far as I've gotten.