obyvatel
The Living Force
From some of the topics in this cognitive science board - like "You Are Not So Smart" and "Thinking, Fast and Slow" we have been acquainted with the topic of cognitive illusions and how our minds are fooled by certain problems and situations. Psychologist Gerd Gigerenzer has a different view than Kahneman regarding the topic of cognitive illusions. What he has to say regarding the nature of gut feelings, how they sometimes work and when they don't, goes into the heart of how we humans make decisions. Decision making touches every aspect of our lives - so the importance of this topic does not need any emphasis. The aim of starting this thread is to have an interactive discussion and deepen our collective understanding of this topic. Gigerenzer's "Risk Savvy:How to Make Good Decisions" and "Gut Feelings: The Intelligence of the Unconscious" are a couple of books that I intend to use as source material.
Let us start with risk and probability (now don't panic if you are not a math whiz). Kahneman showed examples where the mind is fooled by probabilities and mostly left it at that making us feel somewhat stupid and helpless in the face of "cognitive illusions". Gigerenzer shows a method which works quite well in getting unfooled which does not require knowledge of Baye's theorem and base rates. To illustrate this with an example, here is a commonly encountered situation in healthcare:
Mammograms are said to be effective in early detection of breast cancer. The prevalent rate of breast cancer in women is say 10%. A mammogram has 90% chance of detecting cancer incidence correctly. It also has a false positive rate of 9% - that is it can falsely detect cancer when none is actually present. Someone goes for a mammogram and gets a positive result. What is the chance that she has cancer?
A commonly given answer to this question is 90% - several doctors and healthcare professionals give this answer according to Gigerenzer's research. This answer is wrong. Those who have read "Thinking, Fast and Slow" may vaguely recall Kahneman's advice of taking "base rates" into account. But unless one remembers Baye's rule, it is not readily apparent how to solve this problem. Gigerenzer says that the problem with solving the problem is with how the information is presented. The human mind is far more effective in dealing with natural frequencies and counting and can makes sense of the information provided that way instead of dealing directly with probabilities.
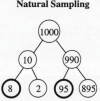
Take a starting number of 1000 women. Of them 10% that is 100 of them are likely to have breast cancer and 90 of them would be correctly identified for the presence of cancer through the mammogram. However, 9% of 1000 - that is 90 of them would show a false positive mammogram. So the chance of actually having cancer diagnosed through a positive mammogram is
90/ (90 +90 ) = 0.5 = 50%.
This kind of information is useful to know since it can help put things in perspective regarding risks and based on research, doctors and healthcare professionals who are advising us are often ignorant about interpreting the numbers correctly. The social cost of having a positive mammogram is not that significant - but a positive HIV test is and people have been known to commit suicide on learning they tested positive.
Moving on, here is something to think about. This example is from a real life game show but we can take the the understanding gained from the example to much more relevant real life situations.
Consider a game where there are 3 closed doors. Behind 2 of the 3 doors there are goats. Behind one door is a grand prize - a cadillac. A participant chooses one of the 3 closed doors. The game show host who knows which door hides what opens a different door to display a goat. Now the participant is given a final choice to stick with what he picked initially or switch. What should he do? In this scenario does switching his choice increase his chances of winning the grand prize (assume he like cadillacs more than goats).
This is a tricky problem. Think for some time before reading on for the answer.
In this situation, the participant has more chance to win the prize if he switches his original choice. It seems counter-intuitive - at least it did to me and I thought that chances are equal for him to win the prize whether he switches his choice or not. Gigerenzer uses a similar strategy of using natural frequency to approach the problem. Consider 3 participants each choosing one of three doors 1, 2 and 3. Door 2 has the cadillac, while 1 and 3 have goats. For the participant choosing door 1, the show host would open door 3 and vice versa. For the participant choosing 2, the show host can open either 1 or 3. Now, for both initial choices of 1 and 3, switching to 2 when given the option would win the prize. Only for the initial choice of 2 - which was the correct choice, switching to 1 or 3 would lose the prize. Since two of our three participants stand to gain from switching, we can conclude that in this situation, a participant increases his chance of winning if he switches his choice.
This problem is known as the Monty Hall problem.
This is the type of problem that can be "solved" using logic. Now consider the case where the game show host does not act in the same way in every situation - and he may even change the parameters.
[quote author=Risk Savvy]
The Monty Hall problem posed by Marilyn and others before her involves a world of risk, not uncertainty . Probability theory provides the best answer only when the rules of the game are certain, when all alternatives, consequences, and probabilities are known or can be calculated.
Here is my question: Is switching also the best choice on the real game show?
The crucial issue is whether Monty always offered his guests the chance to switch. For instance, if Monty were mischievous by nature, he would make the offer only if contestants picked the door with the grand prize behind it. Switching would then always lead to the goat and NBC could keep the big prize for the next show.
[/quote]
The bolded part has implications in decision making in real life and knowing the difference between the "world of risk", where a lot is known, to the "world of uncertainty", where less is known, as it applies to specific situations brings about different strategies. In the world of uncertainty, often simple rules of thumb can outperform complex solutions - as Gigerenzer shows with multiple examples pertaining world of finance (stock picking for example) as well as other more common and regular experiences.
Coming back to the game show example
[quote author=Risk Savvy]
Is the best decision under risk also the best one on the real show? As Monty himself explained, it can be the worst. After one contestant picked door 1, Monty opened door 3, revealing a goat. While the contestant thought about switching to door 2, Monty pulled out a roll of bills and offered $ 3,000 in cash not to switch.
“I’ll switch to it,” insisted the contestant.
“Three thousand dollars,” Monty Hall repeated, “Cash. Cash money. It could be a car , but it could be a goat. Four thousand.”
The contestant resisted the temptation. “I’ll try the door.”
“Forty-five hundred. Forty-seven. Forty-eight. My last offer: Five thousand dollars.”
“Let’s open the door.” The contestant again rejected the offer.
“You just ended up with a goat,” Monty Hall said, opening the door. And he explained: “Now do you see what happened there? The higher I got, the more you thought that the car was behind door 2. I wanted to con you into switching there, because I knew the car was behind 1. That’s the kind of thing I can do when I’m in control of the game.”
In the real game, probability theory is not enough. Good intuitions are needed, which can be more challenging than calculations. One way to reduce uncertainty is to rely on rules of thumb. For instance, the “minimax rule” says:
Choose the alternative that avoids the worst outcome.
Ending up with a goat and foregoing the money is the worst possible outcome. That can only happen if the contestant switches. For that reason, the rule advises taking the money and sticking with door 1. It’s called “minimax” because it aims at minimizing your losses if the maximum loss scenario happens (here, opening the door with a goat). This simple rule would have cut straight through Monty’s psychological game and got the contestant the money— and the car to boot.
Intuitive rules are not foolproof, but neither are calculations. A second way to reduce uncertainty is to guess Monty’s motivation, which is harder, particularly when nervously standing in the spotlight before TV cameras. It requires putting oneself into his mind. Monty appears to have offered the switch because he knew the contestant had chosen the winning door, and then offered money not to switch in order to insinuate that the car was behind the other door. This psychological reflection leads you to stick with your door, the same choice you would make when using the minimax rule.
[/quote]
Finding simple rules which work well in specific environmental conditions relates to the pursuit of ecological rationality. Rather than focusing on the human mind and logic - as Kahneman and others have done in their treatment of cognitive illusions - ecological rationality involves looking at thumb rules or heuristics and how they apply to the human mind and the environment it is operating in. The advantage of using heuristics is that heuristics can apply to real world problems having a natural complexity where an "optimal" (meaning the best possible) solution is often unknown and computationally intractable.
Our unconscious mind uses heuristics. We make mistakes when a heuristic which is supposed to be applied in one environment or situation is misapplied in another situation. Identifying and bringing such rules to consciousness, choosing the right rules from the toolbox and applying them judiciously in keeping with the situation at hand is the goal of ecological rationality.
We are constantly faced with the challenge of making decisions in the face of incomplete and often scarce information - and to be able to navigate this challenge successfully, we need to be able to not only gather inputs from different sources but also learn what to consider as data and what to consider as irrelevant to the context (or noise). This requires a cooperation between rigorous analytical skills as well as intuitive gut feelings and when they work together we get higher degrees of ecological rationality. The quality of gut feelings can be improved - and if Gigerenzer is on the right track, then understanding the rules or heuristics ( for pattern recognition activities) which intuition uses can be of help in this regard.
Let us start with risk and probability (now don't panic if you are not a math whiz). Kahneman showed examples where the mind is fooled by probabilities and mostly left it at that making us feel somewhat stupid and helpless in the face of "cognitive illusions". Gigerenzer shows a method which works quite well in getting unfooled which does not require knowledge of Baye's theorem and base rates. To illustrate this with an example, here is a commonly encountered situation in healthcare:
Mammograms are said to be effective in early detection of breast cancer. The prevalent rate of breast cancer in women is say 10%. A mammogram has 90% chance of detecting cancer incidence correctly. It also has a false positive rate of 9% - that is it can falsely detect cancer when none is actually present. Someone goes for a mammogram and gets a positive result. What is the chance that she has cancer?
A commonly given answer to this question is 90% - several doctors and healthcare professionals give this answer according to Gigerenzer's research. This answer is wrong. Those who have read "Thinking, Fast and Slow" may vaguely recall Kahneman's advice of taking "base rates" into account. But unless one remembers Baye's rule, it is not readily apparent how to solve this problem. Gigerenzer says that the problem with solving the problem is with how the information is presented. The human mind is far more effective in dealing with natural frequencies and counting and can makes sense of the information provided that way instead of dealing directly with probabilities.
Take a starting number of 1000 women. Of them 10% that is 100 of them are likely to have breast cancer and 90 of them would be correctly identified for the presence of cancer through the mammogram. However, 9% of 1000 - that is 90 of them would show a false positive mammogram. So the chance of actually having cancer diagnosed through a positive mammogram is
90/ (90 +90 ) = 0.5 = 50%.
This kind of information is useful to know since it can help put things in perspective regarding risks and based on research, doctors and healthcare professionals who are advising us are often ignorant about interpreting the numbers correctly. The social cost of having a positive mammogram is not that significant - but a positive HIV test is and people have been known to commit suicide on learning they tested positive.
Moving on, here is something to think about. This example is from a real life game show but we can take the the understanding gained from the example to much more relevant real life situations.
Consider a game where there are 3 closed doors. Behind 2 of the 3 doors there are goats. Behind one door is a grand prize - a cadillac. A participant chooses one of the 3 closed doors. The game show host who knows which door hides what opens a different door to display a goat. Now the participant is given a final choice to stick with what he picked initially or switch. What should he do? In this scenario does switching his choice increase his chances of winning the grand prize (assume he like cadillacs more than goats).
This is a tricky problem. Think for some time before reading on for the answer.
In this situation, the participant has more chance to win the prize if he switches his original choice. It seems counter-intuitive - at least it did to me and I thought that chances are equal for him to win the prize whether he switches his choice or not. Gigerenzer uses a similar strategy of using natural frequency to approach the problem. Consider 3 participants each choosing one of three doors 1, 2 and 3. Door 2 has the cadillac, while 1 and 3 have goats. For the participant choosing door 1, the show host would open door 3 and vice versa. For the participant choosing 2, the show host can open either 1 or 3. Now, for both initial choices of 1 and 3, switching to 2 when given the option would win the prize. Only for the initial choice of 2 - which was the correct choice, switching to 1 or 3 would lose the prize. Since two of our three participants stand to gain from switching, we can conclude that in this situation, a participant increases his chance of winning if he switches his choice.
This problem is known as the Monty Hall problem.
This is the type of problem that can be "solved" using logic. Now consider the case where the game show host does not act in the same way in every situation - and he may even change the parameters.
[quote author=Risk Savvy]
The Monty Hall problem posed by Marilyn and others before her involves a world of risk, not uncertainty . Probability theory provides the best answer only when the rules of the game are certain, when all alternatives, consequences, and probabilities are known or can be calculated.
Here is my question: Is switching also the best choice on the real game show?
The crucial issue is whether Monty always offered his guests the chance to switch. For instance, if Monty were mischievous by nature, he would make the offer only if contestants picked the door with the grand prize behind it. Switching would then always lead to the goat and NBC could keep the big prize for the next show.
[/quote]
The bolded part has implications in decision making in real life and knowing the difference between the "world of risk", where a lot is known, to the "world of uncertainty", where less is known, as it applies to specific situations brings about different strategies. In the world of uncertainty, often simple rules of thumb can outperform complex solutions - as Gigerenzer shows with multiple examples pertaining world of finance (stock picking for example) as well as other more common and regular experiences.
Coming back to the game show example
[quote author=Risk Savvy]
Is the best decision under risk also the best one on the real show? As Monty himself explained, it can be the worst. After one contestant picked door 1, Monty opened door 3, revealing a goat. While the contestant thought about switching to door 2, Monty pulled out a roll of bills and offered $ 3,000 in cash not to switch.
“I’ll switch to it,” insisted the contestant.
“Three thousand dollars,” Monty Hall repeated, “Cash. Cash money. It could be a car , but it could be a goat. Four thousand.”
The contestant resisted the temptation. “I’ll try the door.”
“Forty-five hundred. Forty-seven. Forty-eight. My last offer: Five thousand dollars.”
“Let’s open the door.” The contestant again rejected the offer.
“You just ended up with a goat,” Monty Hall said, opening the door. And he explained: “Now do you see what happened there? The higher I got, the more you thought that the car was behind door 2. I wanted to con you into switching there, because I knew the car was behind 1. That’s the kind of thing I can do when I’m in control of the game.”
In the real game, probability theory is not enough. Good intuitions are needed, which can be more challenging than calculations. One way to reduce uncertainty is to rely on rules of thumb. For instance, the “minimax rule” says:
Choose the alternative that avoids the worst outcome.
Ending up with a goat and foregoing the money is the worst possible outcome. That can only happen if the contestant switches. For that reason, the rule advises taking the money and sticking with door 1. It’s called “minimax” because it aims at minimizing your losses if the maximum loss scenario happens (here, opening the door with a goat). This simple rule would have cut straight through Monty’s psychological game and got the contestant the money— and the car to boot.
Intuitive rules are not foolproof, but neither are calculations. A second way to reduce uncertainty is to guess Monty’s motivation, which is harder, particularly when nervously standing in the spotlight before TV cameras. It requires putting oneself into his mind. Monty appears to have offered the switch because he knew the contestant had chosen the winning door, and then offered money not to switch in order to insinuate that the car was behind the other door. This psychological reflection leads you to stick with your door, the same choice you would make when using the minimax rule.
[/quote]
Finding simple rules which work well in specific environmental conditions relates to the pursuit of ecological rationality. Rather than focusing on the human mind and logic - as Kahneman and others have done in their treatment of cognitive illusions - ecological rationality involves looking at thumb rules or heuristics and how they apply to the human mind and the environment it is operating in. The advantage of using heuristics is that heuristics can apply to real world problems having a natural complexity where an "optimal" (meaning the best possible) solution is often unknown and computationally intractable.
Our unconscious mind uses heuristics. We make mistakes when a heuristic which is supposed to be applied in one environment or situation is misapplied in another situation. Identifying and bringing such rules to consciousness, choosing the right rules from the toolbox and applying them judiciously in keeping with the situation at hand is the goal of ecological rationality.
We are constantly faced with the challenge of making decisions in the face of incomplete and often scarce information - and to be able to navigate this challenge successfully, we need to be able to not only gather inputs from different sources but also learn what to consider as data and what to consider as irrelevant to the context (or noise). This requires a cooperation between rigorous analytical skills as well as intuitive gut feelings and when they work together we get higher degrees of ecological rationality. The quality of gut feelings can be improved - and if Gigerenzer is on the right track, then understanding the rules or heuristics ( for pattern recognition activities) which intuition uses can be of help in this regard.