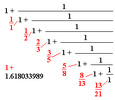
One day, you sit down at your desk, you grab a piece of paper and a pencil, and you start writing down the natural numbers.
1,2,3,4,5,6...
They are very familiar to you. You have known them for a long time.
But now you wonder if there is more to them than meets the eye...
You start adding them, multiplying them, concatenating them, reordering them... anything which comes to your mind.
Your paper becomes crowded with numbers. You are overwhelmed by what you find: very small numbers, very big numbers, even numbers, odd numbers, prime numbers, repeating digits, exponential growth, factorials, geometric continuations, different bases, numbers sharing unique properties, square roots, digital roots, and continued fractions.
After some contemplation, you pick a number sequence near the edge of paper.
1,3,6,10,15,21,...
But you can't quite recall how you found it. So you perform a few operations, but nothing comes close to the sequence.
Thankfully, you are aware of The On-Line Encyclopedia of Integer Sequences (OEIS) and so you type the mysterious sequence into the search bar:
Triangular numbers, how sweet!
Suddenly, you remember how you generated the sequence from 1,2,3,4,5,6:
1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 + 6 = 21
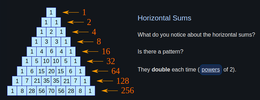
Fantastic, is there a geometrical pattern lurking there?
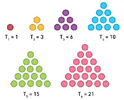
Triangles, triangles everywhere!
You wonder if there is more to it than meets the eye. You apply the same procedure starting from 1,3,6,10,15,21 this time.
1 = 1
1 + 3 = 4
1 + 3 + 6 = 10
1 + 3 + 6 + 10 = 20
1 + 3 + 6 + 10 + 15 = 35
1 + 3 + 6 + 10 + 15 + 21 = 56
You obtain 1,4,10,20,35,56,... the Tetrahedral numbers!
But you continue, you are relentless!
1 = 1
1 + 4 = 5
1 + 4 + 10 = 15
1 + 4 + 10 + 20 = 35
1 + 4 + 10 + 20 + 35 = 70
1 + 4 + 10 + 20 + 35 + 56 = 126
You discover the Pentatope numbers: 1,5,15,35,70,126,...
Hmm.. but how do these sequences fit together?

Pascal's triangle—we meet again!
...and thus we have another starting point, but this time we won't forget where we started from.
1,2,3,4,5,6...
They are very familiar to you. You have known them for a long time.
But now you wonder if there is more to them than meets the eye...
You start adding them, multiplying them, concatenating them, reordering them... anything which comes to your mind.
Your paper becomes crowded with numbers. You are overwhelmed by what you find: very small numbers, very big numbers, even numbers, odd numbers, prime numbers, repeating digits, exponential growth, factorials, geometric continuations, different bases, numbers sharing unique properties, square roots, digital roots, and continued fractions.
After some contemplation, you pick a number sequence near the edge of paper.
1,3,6,10,15,21,...
But you can't quite recall how you found it. So you perform a few operations, but nothing comes close to the sequence.
Thankfully, you are aware of The On-Line Encyclopedia of Integer Sequences (OEIS) and so you type the mysterious sequence into the search bar:
Triangular numbers, how sweet!
Suddenly, you remember how you generated the sequence from 1,2,3,4,5,6:
1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 + 6 = 21
Fantastic, is there a geometrical pattern lurking there?

Triangles, triangles everywhere!
You wonder if there is more to it than meets the eye. You apply the same procedure starting from 1,3,6,10,15,21 this time.
1 = 1
1 + 3 = 4
1 + 3 + 6 = 10
1 + 3 + 6 + 10 = 20
1 + 3 + 6 + 10 + 15 = 35
1 + 3 + 6 + 10 + 15 + 21 = 56
You obtain 1,4,10,20,35,56,... the Tetrahedral numbers!
But you continue, you are relentless!
1 = 1
1 + 4 = 5
1 + 4 + 10 = 15
1 + 4 + 10 + 20 = 35
1 + 4 + 10 + 20 + 35 = 70
1 + 4 + 10 + 20 + 35 + 56 = 126
You discover the Pentatope numbers: 1,5,15,35,70,126,...
Hmm.. but how do these sequences fit together?

Pascal's triangle—we meet again!
...and thus we have another starting point, but this time we won't forget where we started from.