Very often when people talk about the so-called golden ratio, it's all about pentagons, spirals, flowers, monuments, etc.
There is also something about the golden ratio that is quite remarkable. Not only it's an irrational number, it's also the most irrational of the irrational numbers. An irrational is simply a number that cannot be exactly expressed by a ratio on natural numbers, only approximated. Other famous irrational numbers include the square root of 2 (allegedly discovered by the Pythagorean school, but incidentally the "second most irrational" after the golden ratio) and pi. For example, pi can be approximated by 22/7, or 355/113, but not exactly.
Now for the fun part. If an event A occurs periodically at a certain frequency, and another event B occurs periodically at another frequency that's rational to events A's, the two tend to coincide periodically. For instance, the small hand of a clock periodically coincides with the large hand of the clock. In the following representation, the periodical "event" is represented by a cosine function:
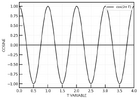
The period is 1. The function reaches the maximum at T = 0, 1, 2, 3, ....., or the minimum at T = 0.5, 1.5, 2.5, .... Basically it repeats itself indefinitely.
No if we add another cosine function at a frequency 3/2 times the first one (2/3 the period), when one accomplishes two cycles, and the other accomplishes three cycles, the sum repeats itself again:
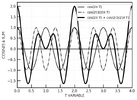
One can count two cycles for the thin continuous line, and three cycles for the thin dashed line, and that corresponds to the thick line (their sum) to accomplish one cycle where the thin lines coincide again.
This behavior is the same for all rational numbers. If one event's frequency is n times another event's frequency (n being rational), they inevitably catch up to each other so to speak.
Now, if the frequency of an event is n times the frequency of another event, and n this time is irrational, their sum is not exactly periodic (maybe cyclical to a certain point) and the two events do not coincide periodically.

One can see that the maximums for instance do not coincide exactly anymore, and always miss each other by a varying "distance".
Of course, this effect is not mathematically reproducible on the computer because of the limit on the of floating numbers accuracy, but one can simply approximate a simple never repeating signal with a very simple trick.
The golden ratio is the limit of the ratio between two subsequent Fibonacci numbers (2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ....). These ratios are of course rational, but it is "irrational at infinity", or for practical purposes when the numbers are large enough for a the effect to be noticeable upon a certain extant.
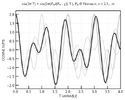
In other words, along the Fibonacci sequence, we transition from periodic to non-periodic event/signals/whatever.
It is fun.
If two planets orbit in such a way, it would be a nightmare for the inhabitants.
However, one could also argue on the other hand that in an atomic world at least, infinite ratios and irrational numbers do not exist really. They are abstractions that represent ratios that are real, which incidentally can all be generated from a variation on the Fibonacci sequence.
There is also something about the golden ratio that is quite remarkable. Not only it's an irrational number, it's also the most irrational of the irrational numbers. An irrational is simply a number that cannot be exactly expressed by a ratio on natural numbers, only approximated. Other famous irrational numbers include the square root of 2 (allegedly discovered by the Pythagorean school, but incidentally the "second most irrational" after the golden ratio) and pi. For example, pi can be approximated by 22/7, or 355/113, but not exactly.
Now for the fun part. If an event A occurs periodically at a certain frequency, and another event B occurs periodically at another frequency that's rational to events A's, the two tend to coincide periodically. For instance, the small hand of a clock periodically coincides with the large hand of the clock. In the following representation, the periodical "event" is represented by a cosine function:

The period is 1. The function reaches the maximum at T = 0, 1, 2, 3, ....., or the minimum at T = 0.5, 1.5, 2.5, .... Basically it repeats itself indefinitely.
No if we add another cosine function at a frequency 3/2 times the first one (2/3 the period), when one accomplishes two cycles, and the other accomplishes three cycles, the sum repeats itself again:

One can count two cycles for the thin continuous line, and three cycles for the thin dashed line, and that corresponds to the thick line (their sum) to accomplish one cycle where the thin lines coincide again.
This behavior is the same for all rational numbers. If one event's frequency is n times another event's frequency (n being rational), they inevitably catch up to each other so to speak.
Now, if the frequency of an event is n times the frequency of another event, and n this time is irrational, their sum is not exactly periodic (maybe cyclical to a certain point) and the two events do not coincide periodically.

One can see that the maximums for instance do not coincide exactly anymore, and always miss each other by a varying "distance".
Of course, this effect is not mathematically reproducible on the computer because of the limit on the of floating numbers accuracy, but one can simply approximate a simple never repeating signal with a very simple trick.
The golden ratio is the limit of the ratio between two subsequent Fibonacci numbers (2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ....). These ratios are of course rational, but it is "irrational at infinity", or for practical purposes when the numbers are large enough for a the effect to be noticeable upon a certain extant.

In other words, along the Fibonacci sequence, we transition from periodic to non-periodic event/signals/whatever.
It is fun.
If two planets orbit in such a way, it would be a nightmare for the inhabitants.
However, one could also argue on the other hand that in an atomic world at least, infinite ratios and irrational numbers do not exist really. They are abstractions that represent ratios that are real, which incidentally can all be generated from a variation on the Fibonacci sequence.
Last edited: