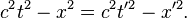An alternative derivation of special relativity

[edwardthefirst]

Also could you elaborate on why you think that:

...we should treat x and x' as the observed wavelength of a light ray, and we should treat t and t' as the observed frequency of the same light ray.

This sounds interesting, but i was just wondering why you thought it was the case.

 

[Archaea]

Hi Archaea,

But to answer your question, my understanding is that v is the relative velocity of the two reference frames. I don't think there is any reason it needs to be c. For that to be the case, it would imply that the two reference frames are always moving away from each other at the speed of light.

As an aside, my background is in computer science, not physics so please bear that in mind when reading my answers. I'm no expert, just someone who finds this fascinating. :)

Hi edwardthefirst,

The problem as I see it is that x, x', t and t' are used in two separate ways. First it's stated that x = ct and x' = ct', then later it's stated that x/t = -v and x'/t' = v. The only way this could be true is if (plus or minus) v is equal to c.

Also could you elaborate on why you think that:

...we should treat x and x' as the observed wavelength of a light ray, and we should treat t and t' as the observed frequency of the same light ray.

This sounds interesting, but i was just wondering why you thought it was the case.

Since it's been stated that x = ct and x' = ct' then x and x' have to be proportional to the observed wavelengths in the reference frames O and O' respectively, while t and t' have to be proportional to the inverse of the observed frequencies. The reason for this is that for light c = λf, where λ is the wavelength and f is the frequency, so the equations x = ct and c = λf must be equivalent, as well as x' = ct' and c = λ'f'.

 

[Archaea]

I've been debating with myself whether or not I should make this post. Lately I've been trying to find a good reason for transformations of inertial reference frames to be rotations in a space-time plane, with the conserved quantity being 4D angular momentum. To do this I decided to start with the equation c = λf instead of x = ct and try to find a linear transformation from (λ, 1/f) to (λ', 1/f'). Since λ and 1/f have different dimensions, I decided to multiply 1/f and 1/f' by c, which just gives λ and λ'. So the linear transformation is:

λ'[1, 1]T = Mλ[1, 1]T

Where M is the transformation matrix, and [1, 1]T is supposed to be a column vector. All this equation means is that M is a matrix which has an Eigenvector [1, 1]T, with an Eigenvalue of λ'/λ. This isn't really very meaningful, but if we decide magically to make the Eigenvectors of M be [1, i]T and [-i, 1]T then M is a 2x2 rotation matrix:

cos θ sin θ
-sin θ cos θ

And the Eigenvalues of M are eiθ and e-iθ which correspond to λ'/λ which is supposed to be the ratio of the observed wavelength of a light ray in two inertial reference frames. This doesn't really make sense, but in quantum mechanics momentum p is equal to hλ, and if we make the angle of rotation θ equal to something like ax, and multiply a plane wave eikx by λ'/λ, then we get ei(k + a)x or ei(k - a)x. So we get a change in momentum by an amount ha.

If you're following this then you're doing well. :)

What I think this means is a light ray with some definite momentum can be in two states, one moving towards the observer represented by the Eigenvector [1, i]T and another moving away from the observer represented by an Eigenvector [-i, 1]T. If a rotation M is applied then the light ray moving towards the observer gains momentum and energy and the light ray moving away loses momentum and energy.

This also fit's in with the idea of the Doppler effect.

Hopefully this might be useful to someone, I personally think that it shows the idea of where I want to go with stuff well, but I'm not convinced that this would be a part of a working theory of physics, which is why I was debating whether or not I should post it. I'll admit that I like it though, because it's weird.

 

[monotonic]

Maybe you can find a program that will allow you to simulate all these possibilities and interact with the result?

 

[Archaea]

Maybe you can find a program that will allow you to simulate all these possibilities and interact with the result?

That's a good idea, but I'm not sure I'm committed enough to physics to do that. I just kind of do this stuff as a hobby. Although if I found a program it would be fun to have a play around with it.

Also I think the stuff in my last post is garbage. I like the idea of a particle having two states, where one state means the particle is moving in the positive direction on some axis, and the other state means the particle is moving in the negative direction. The two states could be in a superposition, where the particle is simultaneously moving in the positive direction and the negative direction. This could happen where, for example, a wave function scatters off a potential wall, and some of the wave function travels through the wall and some of the wave function is deflected back.

However, we don't need the funny magical business from my previous post to do this. All we need is to create two state vectors |x, +> and |x, ->, which represent the particle moving in the positive and negative x directions respectively. Then we can create an operator M which acts on these vectors such that:

M|x, +> = +|x, +>
M|x, -> = -|x, ->

Because this is a two state system, it's analogous to spin.


What I really want to show with this stuff is that the relativistic boost operator is just a rotation operator in a space time plane. I think the way to do this is to use Einstein's ideas and thought experiments in the matrix mechanics formulation of quantum mechanics. I think this would require a fairly comprehensive and implicit understanding of quantum mechanics, which I don't have... yet. :)

 

[Archaea]

OK, it turns out that quantum mechanics already has a way of transforming coordinates. This is done using something called an "inner product." In quantum mechanics the wavefunction ψ(x) is the inner product <x|ψ>, which is really just the dot product of two vectors (<x| and |ψ>) written in a funny way. And to make things worse, these vectors have an uncountably infinite number of elements. But apparently they're still useful, and we can insert the identity Σ|x'><x'| which gives us (assuming <xi|x'j> = δij):

ψ(x) = <x|x'><x'|ψ> = <x|x'>ψ(x')

And likewise:

ψ(x') = <x'|x><x|ψ> = <x'|x>ψ(x)

This is great but the wavefunction needs to be normalized in both reference frames:

1 = ∫ψ(x) dx = ∫<x|x'>ψ(x') dx

So for the wavefunction to be normalized in the x' reference frame:

<x|x'> = dx'/dx

Going the other way around should hopefully give:

<x'|x> = dx/dx'

What's happening here, as far as I can tell, is the amplitude of the wavefunction is being changed by a factor of <x'|x> when transforming from the x reference frame to the x' reference frame. This means the length of the space needs to change by a factor of <x|x'> to keep the wavefunction normalized.

If we now take a look at momentum (ψ(x) has momentum p and ψ(x') has momentum p'):

p'ψ(x') = -iћ (dψ(x')/dx') = -iћ <x'|x> dψ(x)/dx'

Multiplying both sides by dx'/dx:

(dx'/dx)p'ψ(x') = -iћ <x'|x> (dx'/dx) (dψ(x)/dx') = -iћ <x'|x> dψ(x)/dx = <x'|x>pψ(x) = pψ(x')

Which gives:

(dx'/dx)p' = p
p'dx' = pdx

So the length of space is inversely proportional to the momentum. And the transformation between inertial reference frames is just the ratio of relative momenta eigenvalues:

dx'/dx = p/p'

I think a similar thing can be done with the energy operator, and I think that should give the same results.

As always, my work needs to be checked.

 

[Archaea]

I made a mistake, the normalization condition should be ∫|ψ(x)|2 dx or ∫ψ*(x) ψ(x) dx. I'm not sure how things come out now, but I'm certain the equation <x|x'> = dx'/dx is incorrect. Fortunately, this equation isn't really needed and I haven't used it yet anyway.

Continuing on... Doing the same thing with the energy operator as with the momentum operator:

E' ψ(x') = iћ (dψ(x')/dt') = iћ <x'|x> (dψ(x)/dt')

Multiplying both sides by dt'/dt:

(dt'/dt)E'ψ(x') = iћ <x'|x> (dt'/dt) (dψ(x)/dt') = iћ <x'|x> dψ(x)/dt = <x'|x>Eψ(x) = Eψ(x')

Which gives:

(dt'/dt)E' = E
E'dt' = Edt

And:

dt'/dt = E/E'

If this is correct then the observed rates of time evolution of a wavefunction are different by a factor of the ratio of the observed energy of the wavefunction.

If we now take the equation dt'/dt = E/E' multiply it by dx and dividing it by dt' we get:

dx/dt = (dx/dt') E/E'

Multiplying both sides by dx'/dx which is really just p/p':

p/p' dx/dt = (dx'/dt') E/E'

And setting the velocity v = dx/dt and v' = dx'/dt', as well as dividing by p and multiplying by p':

(p/E) v = (p'/E') v'

This equation means that an increase in velocity must be accompanied by a decrease in the p/E ratio, where p and E are the momentum and energy eigenvalues. Also if E = hf and p = h/λ then p/E = 1/fλ, but the velocity of a wave is v = fλ, so the above equation comes out as 1 = 1, which is correct. ;)

This also means that for photons we should get p/E = p'/E', whereas for electrons we should get p/E ≠ p'/E'.

 

[Archaea]

We can create an operator P'μ = (∂xν/∂x'μ) Pν where the P's are momentum operators, and μ and ν run from 0 to 3 and represent the 4 dimensions with P0 being the negative of the energy operator. If we hit this operator with a momentum eigenfunction ψ(x), then we straight away get the elements of the metric tensor:

∂xν/∂x'μ = p'μ/pν

Where p'μ and pν are eigenvalues. This metric tensor transforms from one inertial reference frame to another.

We can do the same thing in the momentum representation of quantum mechanics. Given the position operator xν = iћ ∂/∂pν we can create another operator x'μ = (∂pν/∂p'μ) xν. If we hit this operator with a position eigenfunction ψ(p) we get the elements of the metric tensor in the momentum representation:

∂pν/∂p'μ = x'μ/xν

This equation is a bit hard for me to make sense of, allow me to explain.

Let's say we just want to transform from one Cartesian coordinate frame, with coordinates x, y, and z, to essentially the same coordinate frame, so we can get something like:

∂x/∂y = py/px

This equation essentially says that for every unit the particle moves in the y direction, it moves py/px units in the x direction. This makes sense to me because the particle is moving in a straight line. However in the momentum representation we can get an equation like:

∂py/∂px = x/y

So I think this means that for every unit of momentum gained in the x direction, the particle gains x/y units of momentum in the y direction. This is okay for things like angular momentum and forces, but what do we make x/y be when the particle is just moving in a straight line, and how can this possibly work when x and y represent positions on coordinate axis?

I don't think it makes sense unless there are no position eigenfunctions for particles moving in straight lines.

 

[Archaea]

I've been waiting for a while for my last post to be approved so I can explain why it's wrong.

Firstly, in the equation P'μ = (∂xν/∂x'μ) Pν we need to some over the ν index. This is because three dimensions needs to be confusing. Therefore the equation ∂xν/∂x'μ = p'μ/pν is wrong. As is the equation ∂pν/∂p'μ = x'μ/xν.

Secondly, I'm unclear whether μ and ν should range over from 0 to 3, so the time dimension is included. I think for now they should be changed to i and j, which range from 1 to 3, i.e just the space dimensions, until it can be shown that time can be included. I think if it's possible to show then it could be done using vectors and calculus and stuff. :P

Anyway, I'm still trying to just get the basic stuff out. I'm keen to get to potential energy though. :)

 

[ark]

I've been waiting for a while for my last post to be approved so I can explain why it's wrong.

It is well known that the constancy of the light speed implies the invariance under conformal transformations. Do you know what they are?

 

[Archaea]

I've been waiting for a while for my last post to be approved so I can explain why it's wrong.

It is well known that the constancy of the light speed implies the invariance under conformal transformations. Do you know what they are?

Umm... No.

I ran a Google search for "conformal transformations" and found the Wikipedia page for Conformal map. It say's that:

In mathematics, a conformal map is a function that preserves angles locally.

So I'm guessing that this is somehow related to the invariance of ds2.

If so, I've recently been thinking that the arc length of the path a photon will remain constant under a transformation of inertial reference frames, due to the constancy of the speed of light, while the arc length of the path of an electron will not. Is that obvious though? I'm not sure.

 

[John G]

I ran a Google search for "conformal transformations" and found the Wikipedia page for Conformal map. It say's that:

In mathematics, a conformal map is a function that preserves angles locally.

This Wikipedia page for spherical wave transformations talks about conformal transformations using the speed of light constant:

https://en.wikipedia.org/wiki/Spherical_wave_transformation

 

[shijing]

Conformal transformations are also illustrated in the sixth part of the video series mentioned recently here.

 

[ark]

I've been waiting for a while for my last post to be approved so I can explain why it's wrong.

So I'm guessing that this is somehow related to the invariance of ds2.

No, it is invariance of the condition ds2=0.

Invariance of ds2 implies invariance of ds2=0, but invariance of ds2=0 does not imply invariance of ds2.

 

[Archaea]

I ran a Google search for "conformal transformations" and found the Wikipedia page for Conformal map. It say's that:

In mathematics, a conformal map is a function that preserves angles locally.

This Wikipedia page for spherical wave transformations talks about conformal transformations using the speed of light constant:

https://en.wikipedia.org/wiki/Spherical_wave_transformation

Thanks for the link Bluelamp, I read some of it. I'm interested to know whether the Lorentz transformations can be derived using these transformations. In the article they seem to do something, but I wasn't able to follow.

I also found this Wikipedia page: Derivations of the Lorentz transformations. If you scroll down to the section "Einstein's popular derivation" you'll see the mistake where it's said that x = ct and then latter the equation x = vt is used, I'm fairly sure this would mean that v = c. :) In the "Spherical wavefronts of light" section there's the same mistake as well as in the "Landau & Lifshitz solution" section.

The "Landau & Lifshitz solution" is interesting, however, because they start with the equation:

And solve it somehow to get the hyperbolic rotation:

However, if we change the first equation to c2t2 + (ix)2 = c'2t'2 + (ix')2 then we get a regular rotation in the complex plane.

Conformal transformations are also illustrated in the sixth part of the video series mentioned recently here.

Thanks for the link Shijing, I watched the first part and will watch the rest later. :)

I've been waiting for a while for my last post to be approved so I can explain why it's wrong.

So I'm guessing that this is somehow related to the invariance of ds2.

No, it is invariance of the condition ds2=0.

Invariance of ds2 implies invariance of ds2=0, but invariance of ds2=0 does not imply invariance of ds2.

Hi Ark, I'm not sure I fully understand, I tried finding something on Wikipedia, but I'm afraid it might be beyond me ATM. Does it mean that a light-like path has zero "distance" in space-time, but this doesn't imply that a time-like path has zero "distance" in space-time?

At any rate, there's a rumor going around that you're a real life physicist, so I have some questions. These are just yes or no questions and if you've read my other posts in this thread then they shouldn't be new.

Q1) IIRC For a one dimensional wave function, there's the equation ψ(x) = <x|ψ>. Does this mean that we can insert the identity Σ|x'><x'| (which for one dimension should just be |x'><x'|) into that equation to get the transformation equation ψ(x) = <x|x'><x'|ψ> = <x|x'> ψ(x')? This would mean a change in the amplitude of the wave function when transforming coordinates. Also would the inner product <x|x'> be just a number?

Q2) Can we transform the momentum operator such that: (for space coordinates only) P'i = (∂xj/∂x'i) Pj? I'm a bit concerned that for some reason the RHS might not fit the definition of an operator.

Q3) This is probably my favorite question. :) For a three dimensional separable wave function: ψ(x, y, z) = ψ(x)ψ(y)ψ(z) is it true that:

?

My thinking is that we can pull ψ(y)ψ(z) and ψ*(y)ψ*(z) out of the x integral as constants, then we can pull ∫ψ*(x)ψ(x)dx out of the y and z integrals as a constant, then repeat the same thing with the y intergral.

Q4) If we ignore the Schrödinger equation, so that energy doesn't need to be proportional to the square of the momentum, can we change the momentum operator to be P = iћ (d/dx)? So that we drop the minus sign.