Guys, I think you might be interested in this:
With a stunningly simple proof, a researcher has finally cracked the sensitivity conjecture, "one of the most frustrating and embarrassing open problems."
www.wired.com
There’s even a quantum physics version of query complexity in which the banker can ask a “superposition” of several questions at the same time. Figuring out how this measure relates to other complexity measures has helped researchers understand the
limitations of quantum algorithms.
Cornering the Solution
Huang heard about the sensitivity conjecture in late 2012, over lunch with the mathematician
Michael Saks at the Institute for Advanced Study, where Huang was a postdoctoral fellow.[...] Huang knew, as did the broader research community, that the sensitivity conjecture could be settled if mathematicians could prove an easily stated conjecture about collections of points on cubes of different dimensions.
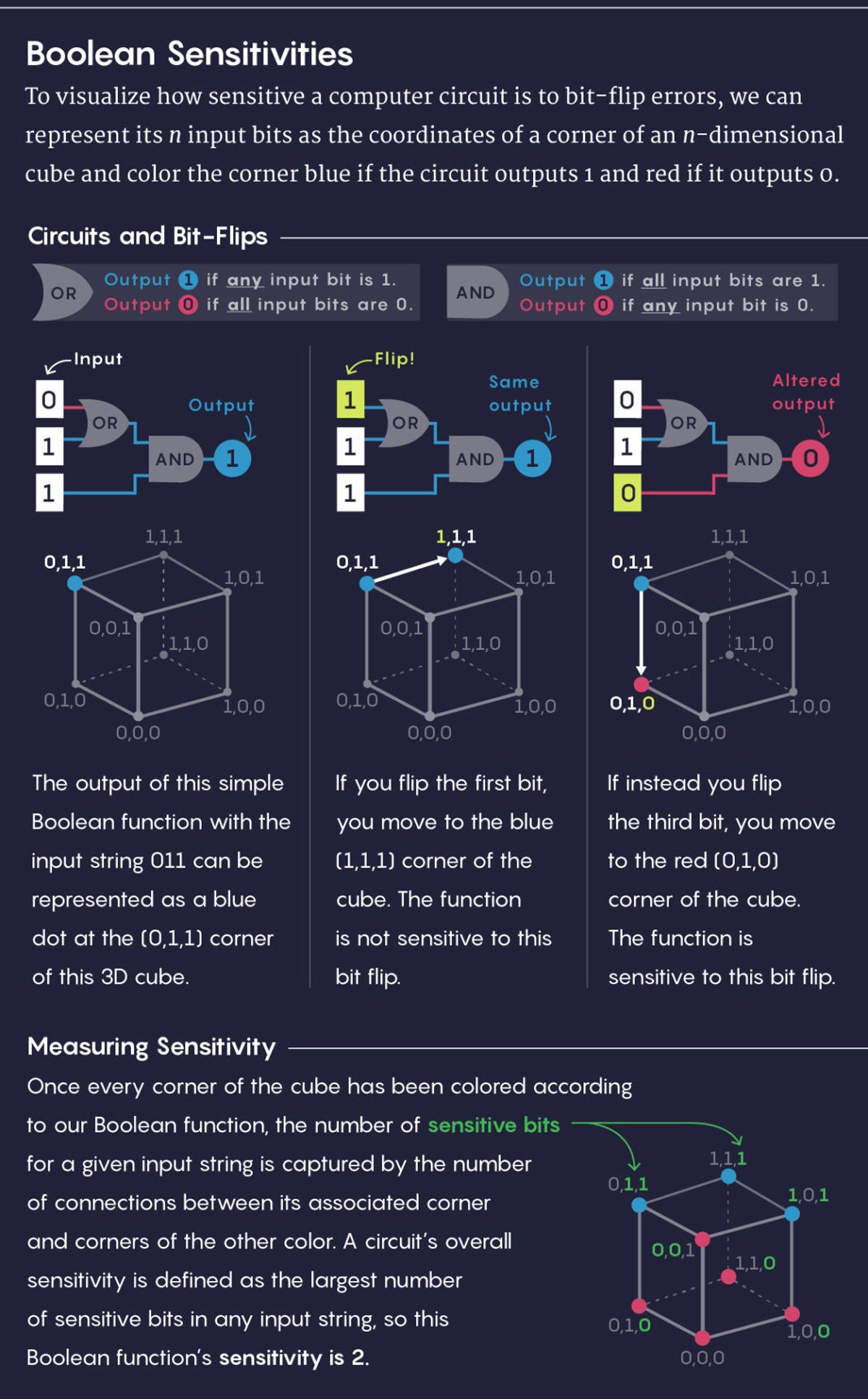
There’s a natural way to go from a string of n 0s and 1s to a point on an n-dimensional cube: Simply use the n bits as the coordinates of the point.
For instance, the four two-bit strings—00, 01, 10 and 11—correspond to the four corners of a square in the two-dimensional plane: (0,0), (0,1), (1,0) and (1,1). Likewise, the eight three-bit strings correspond to the eight corners of a three-dimensional cube, and so on in higher dimensions. A Boolean function, in turn, can be thought of as a rule for coloring these corners with two different colors (say, red for 0 and blue for 1).
In 1992,
Craig Gotsman, now of the New Jersey Institute of Technology, and
Nati Linial of Hebrew University
figured out that proving the sensitivity conjecture can be reduced to answering a simple question about cubes of different dimensions: If you choose any collection of more than half the corners of a cube and color them red, is there always some red point that is connected to many other red points? (Here, by “connected,” we mean that the two points share one of the outer edges of the cube, as opposed to being across a diagonal.)
If your collection contains exactly half the corners of the cube, it’s possible that none of them will be connected. For example, among the eight corners of the three-dimensional cube, the four points (0,0,0), (1,1,0), (1,0,1) and (0,1,1) all sit across diagonals from one another. But as soon as more than half the points in a cube of any dimension are colored red, some connections between red points must pop up. The question is: How are these connections distributed? Will there be at least one highly connected point?
In 2013, Huang started thinking that the best route to understanding this question might be through the standard method of representing a network with a matrix that tracks which points are connected and then examining a set of numbers called the matrix’s eigenvalues. For five years he kept revisiting this idea, without success. “But at least thinking about it [helped] me quickly fall asleep many nights,” he
commented on Aaronson’s blog post.
Then in 2018, it occurred to Huang to use a 200-year-old piece of mathematics called the Cauchy interlace theorem, which relates a matrix’s eigenvalues to those of a submatrix,
making it potentially the perfect tool to study the relationship between a cube and a subset of its corners. Huang decided to request a grant from the National Science Foundation to explore this idea further.
Then last month, as he sat in a Madrid hotel writing his grant proposal,
he suddenly realized that he could push this approach all the way to fruition simply by switching the signs of some of the numbers in his matrix. In this way, he was able to prove that in any collection of more than half the points in an
n-dimensional cube, there will be some point that is connected to at least the square-root-of-n of the other points—and the sensitivity conjecture instantly followed from this result.
vfrdtyky.blogspot.com
protons and electrons - not even containing neutrons in my initial model. No Weak Force, no Strong Force! Just Electrostatics (and Gravity), and wave functions in a close-packed crystalline form.
