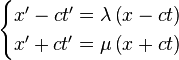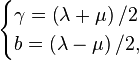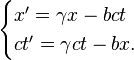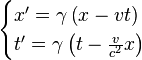An alternative derivation of special relativity

[John G]

Thanks for the link Bluelamp, I read some of it. I'm interested to know whether the Lorentz transformations can be derived using these transformations. In the article they seem to do something, but I wasn't able to follow.

I also found this Wikipedia page: Derivations of the Lorentz transformations. If you scroll down to the section "Einstein's popular derivation" you'll see the mistake where it's said that x = ct and then latter the equation x = vt is used, I'm fairly sure this would mean that v = c. :) In the "Spherical wavefronts of light" section there's the same mistake as well as in the "Landau & Lifshitz solution" section.

The "Landau & Lifshitz solution" is interesting, however, because they start with the equation:

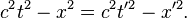
And solve it somehow to get the hyperbolic rotation:

However, if we change the first equation to c2t2 + (ix)2 = c'2t'2 + (ix')2 then we get a regular rotation in the complex plane.

The v is just for a massive particle reference frame and they are doing calculations useful for time dilation and length contraction so you don't want to make v=c. For adding the imaginary i, you add that for the radius which in this case should be time which after squaring just makes it negative. That is confusing in places for these Wiki pages cause time seems to have the wrong sign if you aren't careful.

Thanks for the link Shijing, I watched the first part and will watch the rest later. :)

Yeah that was good, I somehow missed it even though I was here on this forum back then. That kind of drives home the idea that special conformal transformations can be thought of as inversions (with translations) which isn't weird at all (but fun to view) if you are just doing it spatially but if you are inverting space and time (reciprocal-like) things get weird (and they do like near black holes or if you are modeling tachyons).

Hi Ark, I'm not sure I fully understand, I tried finding something on Wikipedia, but I'm afraid it might be beyond me ATM. Does it mean that a light-like path has zero "distance" in space-time, but this doesn't imply that a time-like path has zero "distance" in space-time?

That's just the zero from that very first equation on your Derivations of the Lorentz transformations Wiki page:
c2(t2-t1)2-(x2-x1)2-(y2-y1)2-(x2-x1)2=0

 

[John G]

I'm interested to know whether the Lorentz transformations can be derived using these transformations. In the article they seem to do something, but I wasn't able to follow.

Forgot to say something for this part. The Lorentz group is a subgroup of the conformal group hence it's used where there's been a symmetry break from conformal symmetry. For the spherical wave transformations you are basically doing a reciprocal of the right hand side of the equation when doing the conformal transformation version instead of the Lorentz transformation version.

 

[Archaea]

The v is just for a massive particle reference frame and they are doing calculations useful for time dilation and length contraction so you don't want to make v=c. For adding the imaginary i, you add that for the radius which in this case should be time which after squaring just makes it negative. That is confusing in places for these Wiki pages cause time seems to have the wrong sign if you aren't careful.

What I mean is that for the mathematics to be consistent we need to have v = c. I think it helps to think a bit like a high school maths student in order to see it. If we take the "Einstein's popular derivation" section from the derivations of the Lorentz transformations Wikipedia page:

In his popular book[4] Einstein derived the Lorentz transformation by arguing that there must be two non-zero coupling constants λ and μ such that

that correspond to light traveling along the positive and negative x-axis, respectively. For light x = ct if and only if x′ = ct′. Adding and subtracting the two equations and defining

gives

Substituting x′ = 0 corresponding to x = vt and noting that the relative velocity is v = bc/γ, this gives

The constant γ can be evaluated by demanding c2t2 − x2 = c2t'2 − x'2 as per standard configuration.

Now we can put some numbers into these equations: let c = 3, and t = 5, and so x = 15. The first equation is x' - ct' = λ(x - ct), we can just ignore this equation because no matter what λ is, x - ct is 0 and so x' - ct' = 0. For the second equation, let μ = 2, so x' + ct' = μ(x + ct) = 2 * (15 + 15) = 30.

For the third and forth equations we may as well just let λ stay as λ. We get:

γ = (λ + μ) / 2 = λ/2 + 1
b = (λ - μ) / 2 = λ/2 - 1

Which gives equations 5 and 6:

x' = γx - bct = (λ/2 + 1) * 15 - (λ/2 - 1) * 15 = 15 + 15 = 30
ct' = γct - bx = (λ/2 + 1) * 15 - (λ/2 - 1) * 15 = 15 + 15 = 30

Now it says that we need to set x' = 0 corresponding to x = vt. This means we need to go back to the start, if x' is 0 then ct' is zero, because x' = ct', now μ needs to be 0 due to the second equation x' + ct' = 0 = μ (x + ct) = 30μ and so the third equation equals the forth equation, which means γ = b. So if the velocity is v = bc/γ, then v = c which is good because we used the two equations x = ct and x = vt and they need to be consistent with each other in order for mathematics to work properly.

I haven't checked all the derivations, but the ones I have looked at all start off with x = ct and then switch to x = vt somewhere in the middle.

 

[John G]

For some of those equations if you let v=c, you end up dividing by zero. It's certainly OK to think about the idea of reference frames moving at the speed of light; you could actually come to the conclusion that massless particle beings would perceive a complete worldline through a universe state all at once. You might also need the full conformal group instead of just the Lorentz group if you want to explore reference frames at the speed of light and above:

http://www.researchgate.net/publication/226071540_A_new_unified_approach_to_bradyons_and_tachyons_by_conformal_transformations

 

[Archaea]

For some of those equations if you let v=c, you end up dividing by zero. It's certainly OK to think about the idea of reference frames moving at the speed of light; you could actually come to the conclusion that massless particle beings would perceive a complete worldline through a universe state all at once. You might also need the full conformal group instead of just the Lorentz group if you want to explore reference frames at the speed of light and above:

http://www.researchgate.net/publication/226071540_A_new_unified_approach_to_bradyons_and_tachyons_by_conformal_transformations

I think you're right about dividing by zero if v=c. Also I think the Lorentz transformations aren't the correct transformations for going between inertial reference frames. I've convinced myself of this, but convincing others is a different beast entirely.

Anyway, I found a better way to show that v and c must be equal in the "Einstein's popular derivation" derivation. If we look at equations 5 and 6, which are:

x' = γx - bct
t' = γct - bx

And let t' = 0 when x' = 0 (which we can always do AFAIK) then at that point:

0 = γx - bct
0 = γct - bx

v = x/t = bc/γ
v = x/t = γc/b

Therefore b = γ, and v = c.

 

[Archaea]

While thinking about my last post in this thread it occurred to me that if the origins of the two inertial reference frames are the same then it doesn't necessarily mean that v = c. Fortunately, I think I've found a better way. If we look at the last set of equations form the "Einstein's popular derivation" derivation:

And solve for t in the first equation to get:

t = x/v - x'/vγ

And substitute this into the second equation:

t' = γ(x/v - x'/vγ - vx/c2)
t' = γx(1/v - v/c2) - x'/v

OK I think I made a mistake... But the upshot is that if x' = -vt' (which I'm not sure about) then:

1/v - v/c2 = 0
v2 = c2

I think this would be nice if it were true because then it's possible to show any derivation of SR is mathematically inconsistent.

 

[Ronan]

I was studying a youtube course on linear algebra earlier this year. Look up N J Wildberger. There is a video series WildLinAlg. InVideos 37-39 he gives a rather novel introduction to Special Relativity. A lot of what he lectures is based on what he calls Rational Trigonometry. This is an algebraic approach to Trig. I cam across that about 3 years ago and like the approach. I found the SR lectures very fascinitating especially as I wasn't really willing to get involved with understanding the padadoxes that arise in the subject. He gives a very understandable explination of the twins paradox based on coordinate systems.

 

[Archaea]

I was studying a youtube course on linear algebra earlier this year. Look up N J Wildberger. There is a video series WildLinAlg. InVideos 37-39 he gives a rather novel introduction to Special Relativity. A lot of what he lectures is based on what he calls Rational Trigonometry. This is an algebraic approach to Trig. I cam across that about 3 years ago and like the approach. I found the SR lectures very fascinitating especially as I wasn't really willing to get involved with understanding the padadoxes that arise in the subject. He gives a very understandable explination of the twins paradox based on coordinate systems.

Thanks for the videos, I watched the first two. I found it interesting that SR can be derived using bats for observers and sound instead of light. I don't know if he explains this in the third video, but for his bat example, bat A is stationary to the medium for sound, whereas bat B is moving relative to the medium, this means that they observe different velocities for the speed of sound. If the speed of light is observed to be the same by two observers in outer space, even if they're moving relative to each other, they'll still observe themselves to be stationary to the medium for light.

For this reason I think N J Wildberger has done a better job than me in showing the incorrectness of SR. It's amusing to think of bats in a cave discussing the impossibility of anything entering their cave because all other caves are so far away, and nothing can travel faster than the speed of sound. ;)