DiscoveringTruth
Padawan Learner
I read a very interesting article a few months ago while researching about characterization of psychedelic experiences which lies at the intersection of "Inner and Outer Sciences". I am interested in understanding the nature of mystical or psychedelic experiences and what they may reveal about the hyper-dimensional nature of the universe.
DMT in particular it seems can reveal an objectively deeper, hidden, hyper dimensional nature of reality which is vastly different from everyday experience. I feel DMT research in particular is going to bear more fruit in this regard because DMT experiences are the furthest removed from ordinary reality among those offered by other psychedelic drugs (such as peyote, mushrooms, LSD). DMT experiences are more vivid and many people who come out of the experience talk about meeting entities, seeing mathematical structures such as a torus room with an entity in the middle, and a profound lack of sense of time which is interesting considering that the Cs say time doesn't exist.
If one disregards the idea that DMT is just a hallucination fabricated by the mind (for materialists, even normal waking reality is a hallucination made up by the brain), and observes the DMT space with a mathematically trained eye, one may be surprised to find that the experience seems to occur in a space which follows more and more non-Euclidean hyperbolic geometry principles as the dosage of DMT increases. To be clear, I am not proposing anyone take DMT to test this out since DMT can trigger a highly uncontrolled experience dependent on mood and beliefs of the person but my intent is to glean whatever interesting information I can from people who have taken the substance and have tried to understand the phenomenon from a mathematical perspective. The article (linked below) proposes a way to characterize the experience of the DMT space mathematically, which is a unique approach to the phenomenon and I am hopeful that further research in this direction will reveal even more information about hyperspaces and perhaps even other densities someday. I hope this may even be useful to @ark as he strives to build a mathematical framework for concepts of consciousness, UFT etc.
Here is the full article referenced in the para earlier - The Hyperbolic Geometry of DMT experiences. Here is a snippet from the article -
The article goes in greater depth than this snippet and may be difficult to understand on a first read. Here is a simpler ELI5 (Explain it to me Like I'm 5yrs old) version of the original article by the same author - ELI5 “The Hyperbolic Geometry of DMT Experiences”
From another article on the same website - Algorithmic Reduction of Psychedelic States
Wanted to share in light of @ark's recent April 2022 Cassiopaean session discussion. Happy to hear your thoughts!
DMT in particular it seems can reveal an objectively deeper, hidden, hyper dimensional nature of reality which is vastly different from everyday experience. I feel DMT research in particular is going to bear more fruit in this regard because DMT experiences are the furthest removed from ordinary reality among those offered by other psychedelic drugs (such as peyote, mushrooms, LSD). DMT experiences are more vivid and many people who come out of the experience talk about meeting entities, seeing mathematical structures such as a torus room with an entity in the middle, and a profound lack of sense of time which is interesting considering that the Cs say time doesn't exist.
If one disregards the idea that DMT is just a hallucination fabricated by the mind (for materialists, even normal waking reality is a hallucination made up by the brain), and observes the DMT space with a mathematically trained eye, one may be surprised to find that the experience seems to occur in a space which follows more and more non-Euclidean hyperbolic geometry principles as the dosage of DMT increases. To be clear, I am not proposing anyone take DMT to test this out since DMT can trigger a highly uncontrolled experience dependent on mood and beliefs of the person but my intent is to glean whatever interesting information I can from people who have taken the substance and have tried to understand the phenomenon from a mathematical perspective. The article (linked below) proposes a way to characterize the experience of the DMT space mathematically, which is a unique approach to the phenomenon and I am hopeful that further research in this direction will reveal even more information about hyperspaces and perhaps even other densities someday. I hope this may even be useful to @ark as he strives to build a mathematical framework for concepts of consciousness, UFT etc.
Here is the full article referenced in the para earlier - The Hyperbolic Geometry of DMT experiences. Here is a snippet from the article -
What about DMT suggests hyperbolic geometry?
Why should we believe that phenomenal space on DMT (and to a lesser extent on other psychedelics) becomes hyperbolic-like? We will argue that the features people use to describe their trips as well as concrete mathematical observations of such features point directly to hyperbolic geometry. Here is a list of such features (arranged from least to most suggestive… you know, for dramatic effect):
This article goes beyond claiming a mere connection between DMT and hyperbolic geometry. We will be more specific by addressing the aspects of the experience that can be interpreted geometrically. To do so, let us now turn to a phenomenological description of the way DMT experiences usually unfold:
- Perception of far-out travel (as we said, small movements in hyperbolic space lead to huge changes in the scene).
- Feelings of becoming big (you can fit a lot more inside a circle of radius r in hyperbolic space).
- The space experienced is often depicted as “more real and more dense than normal”.
- The use of terms like “mind-expanding” and “warping” to describe the effects of the drug are very common.
- People describing it as “a different kind of space” and frequently using the word “hyperspace” to talk about it.
- Difficulty integrating/remembering the objects and scenes experienced (e.g. “they were too alien to recall”).
- Constant movement/acceleration and change of perspectives which are often described as “unfolding scenes and expanding patterns” (cf. the chrysanthemum, jitterbox).
- Continuous change of the scene’s context through escape routes: A door that leads to a labyrinth that leads to branching underground tunnels that lead to mirror rooms that lead to endless windows, and the one you take leading you to a temple with thirty seven gates which lead you to a kale salad world etc. (example).
- Crowding of scene beyond the limits of Euclidean space (users frequently wondering “How was I able to fit so much in my mind? I don’t see any space for my experience to fit in here!”)
- Reported similarity with fractals.
- Omnipresence of saddles making up the structural constraints of the hallucinated scenes. For example, one often hears about experiencing scenes saturated with: joints, twists, bifurcations, curved alleys, knots, and double helixes.
- Looking at self-similar objects (such as cauliflowers) can get you lost in what seems like endless space. (Note: beware of the potential side effects of looking at a cauliflower on DMT*).
- PSIS-like experiences where people seem to experience multiple alternative outcomes from each event at the same time (this may be the result of “hyperbolic branching” through time rather than space).
- Psychedelic replication pictures usually include features that can be interpreted as hyperbolic objects embedded in Euclidean 3D.
- People describe “incredibly advanced mechanisms” and “impossible objects” that cannot be represented in our usual reality (e.g. Terence Mckenna’s self-dribbling basketballs).
- At least one mathematician has stated that what one experiences on DMT cannot be translated into Euclidian geometry (unlike what one experiences on LSD).
- We received a series of systematic DMT trip-reports by a math enthusiast and experienced psychonaut who claims that the surfaces experienced on DMT are typically composed of hyperbolic tilings (which imply a negative curvature; cf. wallpaper groups).
The Phenomenology of DMT experiences: The 6 Levels
In order to proceed we will give an account of a typical vaporized DMT experience. You can think of the following six sections as stages or levels of a DMT journey. Let me explain. The highest level you get to depends on the dose consumed, and in high doses one experiences all of the levels, one at a time, and in quick succession (i.e. on high doses these levels are perceived as the stages of the experience). If one takes just enough DMT to cross over to the highest level one reaches during the journey for only a brief moment, then that level will probably be described as “the peak of the experience”. If, on the other hand, one takes a dose that squarely falls within the milligram range for producing a given level, it will be felt as more of a “plateau”. Each level is sufficiently distinct from the others that people will rarely miss the transitions between them.
The six levels of a DMT experience are: Threshold, Chrysanthemum, Magic Eye, Waiting Room, Breakthrough, and Amnesia. Let us dive in!
(Note: The following description assumes that the self-experimenter is in good physical and mental health at the time of consuming the DMT. It is well known that negative states of consciousness can lead to incomprehensible hellscapes when “boosted” by DMT (please avoid DMT at all costs while you are drunk, depressed, angry, suicidal, irritable, etc.). The full geometry is best appreciated on a mentally and emotionally balanced set and settings.)
The article goes in greater depth than this snippet and may be difficult to understand on a first read. Here is a simpler ELI5 (Explain it to me Like I'm 5yrs old) version of the original article by the same author - ELI5 “The Hyperbolic Geometry of DMT Experiences”
ELI5 “The Hyperbolic Geometry of DMT Experiences”
Posted on May 28, 2017 by algekalipso
I wrote the following in response to a comment on the r/RationalPsychonaut subreddit about this DMT article I wrote some time ago. The comment in question was: “Can somebody eli5 [explain like I am 5 years old] this for me?” So here is my attempt (more like “eli12”, but anyways):
In order to explain the core idea of the article I need to convey the main takeaways of the following four things:
- Differential geometry,
- How it relates to symmetry,
- How it applies to experience, and
- How the effects of DMT turn out to be explained (in part) by changes in the curvature of one’s experience of space (what we call “phenomenal space”).
1) Differential Geometry
If you are an ant on a ball, it may seem like you live on a “flat surface”. However, let’s imagine you do the following: You advance one centimeter in one direction, you turn 90 degrees and walk another centimeter, turn 90 degrees again and advance yet another centimeter. Logically, you just “traced three edges of a square” so you cannot be in the same place from which you departed. But let’s says that you somehow do happen to arrive at the same place. What happened? Well, it turns out the world in which you are walking is not quite flat! It’s very flat from your point of view, but overall it is a sphere! So you ARE able to walk along a triangle that happens to have three 90 degree corners.
That’s what we call a “positively curved space”. There the angles of triangles add up to more than 180 degrees. In flat spaces they add up to 180. And in “negatively curved spaces” (i.e. “negative Gaussian curvature” as talked about in the article) they add up to less than 180 degrees.

Eight 90-degree triangles on the surface of a sphere
So let’s go back to the ant again. Now imagine that you are walking on some surface that, again, looks flat from your restricted point of view. You walk one centimeter, then turn 90 degrees, then walk another, turn 90 degrees, etc. for a total of, say, 5 times. And somehow you arrive at the same point! So now you traced a pentagon with 90 degree corners. How is that possible? The answer is that you are now in a “negatively curved space”, a kind of surface that in mathematics is called “hyperbolic”. Of course it sounds impossible that this could happen in real life. But the truth is that there are many hyperbolic surfaces that you can encounter in your daily life. Just to give an example, kale is a highly hyperbolic 2D surface (“H2” for short). It’s crumbly and very curved. So an ant might actually be able to walk along a regular pentagon with 90-degree corners if it’s walking on kale (cf. Too Many Triangles).

An ant walking on kale may infer that the world is an H2 space.
In brief, hyperbolic geometry is the study of spaces that have this quality of negative curvature. Now, how is this related to symmetry?
2) How it relates to symmetry
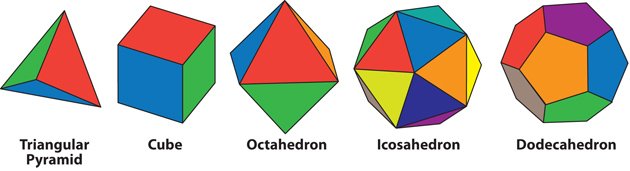
As mentioned, on the surface of a sphere you can find triangles with 90 degree corners. In fact, you can partition the surface of a sphere into 8 regular triangles, each with 90 degree corners. Now, there are also other ways of partitioning the surface of a sphere with regular shapes (“regular” in the sense that every edge has the same length, and every corner has the same angle). But the number of ways to do it is not infinite. After all, there’s only a handful of regular polyhedra (which, when “inflated”, are equivalent to the ways of partitioning the surface of a sphere in regular ways).
If you instead want to partition a plane in a regular way with geometric shapes, you don’t have many options. You can partition it using triangles, squares, and hexagons. And in all of those cases, the angles on each of the vertices will add up to 360 degrees (e.g. six triangles, four squares, or thee corners of hexagons meeting at a point). I won’t get into Wallpaper groups, but suffice it to say that there are also a limited number of ways of breaking down a flat surface using symmetry elements (such as reflections, rotations, etc.).
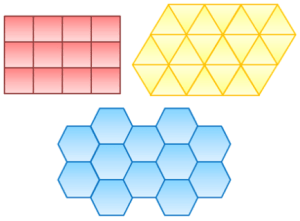
Regular tilings of 2D flat space
Hyperbolic 2D surfaces can be partitioned in regular ways in an infinite number of ways! This is because we no longer have the constraints imposed by flat (or spherical) geometries where the angles of shapes must add up to a certain number of degrees. As mentioned, in hyperbolic surfaces the corners of triangles add up to less than 180 degrees, so you can fit more than 6 corners of equilateral triangles at one point (and depending on the curvature of the space, you can fit up to an infinite number of them). Likewise, you can tessellate the entire hyperbolic plane with heptagons.
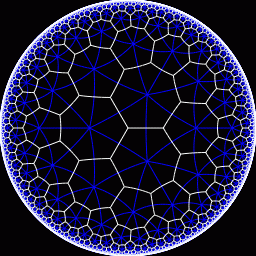
Hyperbolic tiling: Each of the heptagons is just as big (i.e. this is a projection of the real thing)
On the flip side, if you see a regular partitioning of a surface, you can infer what its curvature is! For example, if you see that a surface is entirely covered with heptagons, three on each of the corners, you can be sure that you are seeing a hyperbolic surface. And if you see a surface covered with triangles such that there are only four triangles on each joint, then you know you are seeing a spherical surface. So if you train yourself to notice and count these properties in regular patterns, you will indirectly also be able to determine whether the patterns inhabit a spherical, flat, or hyperbolic space!
3) How it applies to experience
How does this apply to experience? Well, in sober states of consciousness one is usually restricted to seeing and imagining spherical and flat surfaces (and their corresponding symmetric partitions). One can of course look at a piece of kale and think “wow, that’s a hyperbolic surface” but what is impossible to do is to see it “as if it were flat”. One can only see hyperbolic surfaces as projections (i.e. where we make regular shapes look irregular so that they can fit on a flat surface) or we end up contorting the surface in a crumbly fashion in order to fit it in our flat experiential space. (Note: even sober phenomenal space happens to be based on projective geometry; but let’s not go there for now.)
4) DMT: Hyperbolizing Phenomenal Space
In psychedelic states it is common to experience whatever one looks at (or, with more stunning effects, whatever one hallucinates in a sensorially-deprived environment such as a flotation tank) as slowly becoming more and more symmetric. Symmetrical patterns are attractors in psychedelia. It’s common for people to describe their acid experiences as “a kaleidoscope of colors and meaning”. We should not be too quick to dismiss these descriptions as purely metaphorical. As you can see from the article Algorithmic Reduction of Psychedelic States as well as PsychonautWiki’s Symmetrical Texture Repetition, LSD and other psychedelics do in fact “symmetrify” the textures you experience!

What gravel might look like on 150 mics of LSD (Source)
As it turns out, this symmetrification process (what we call “lowering the symmetry detection/propagation threshold”) does allow one to experience any of the possible ways of breaking down spherical and flat surfaces in regular ways (in addition to also enabling the experience of any wallpaper group!). Thus the surfaces of the objects one hallucinates on LSD (specially for Closed Eyes Visuals), are usually carpeted with patterns that have either spherical or flat symmetries (e.g. seeing honeycombs, square grids, regular triangulations, etc.; or seeing dodecahedra, cubes, etc.).

17 wallpaper symmetry groups
Only on very high doses of classic psychedelics does one start to experience objects that have hyperbolic curvature. And this is where DMT becomes very relevant. Vaping it is one of the most efficient ways of achieving “unworldly levels of psychedelia”:
On DMT the “symmetry detection threshold” is reduced to such an extent that any surface you look at very quickly gets super-saturated with regular patterns. Since (for reasons we don’t understand) our brain tries to incorporate whatever shape you hallucinate into the scene as part of the scene, the result of seeing too many triangles (or heptagons, or whatever) is that your brain will “push them into the surfaces” and, in effect, turn those surfaces into hyperbolic spaces.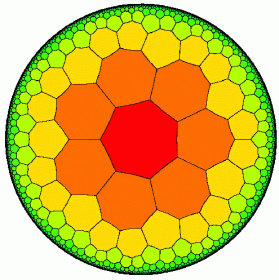
Yet another part of your brain (or system of consciousness, whatever it turns out to be) recognizes that “wait, this is waaaay too curved somehow, let me try to shape it into something that could actually exist in my universe”. Hence, in practice, if you take between 10 and 20 mg of DMT, the hyperbolic surfaces you see will become bent and contorted (similar to the pictures you find in the article) just so that they can be “embedded” (a term that roughly means “to fit some object into a space without distorting its properties too much”) into your experience of the space around you.
But then there’s a critical point at which this is no longer possible: Even the most contorted embeddings of the hyperbolic surfaces you experience cannot fit any longer in your normal experience of space on doses above 20 mg, so your mind has no other choice but to change the curvature of the 3D space around you! Thus when you go from “very high on DMT” to “super high on DMT” it feels like you are traveling to an entirely new dimension, where the objects you experience do not fit any longer into the normal world of human experience. They exist in H3 (hyperbolic 3D space). And this is in part why it is so extremely difficult to convey the subjective quality of these experiences. One needs to invoke mathematical notions that are unfamiliar to most people; and even then, when they do understand the math, the raw feeling of changing the damn geometry of your experience is still a lot weirder than you could ever anticipate.

Anybody else want to play hyperbolic soccer? Humans vs. Entities, the match of the eon!
Note: The original article goes into more depth
Now that you understand the gist of the original article, I encourage you to take a closer look at it, as it includes content that I didn’t touch in this ELI5 (or 12) summary. It provides a granular description of the 6 levels of DMT experience (Threshold, Chrysanthemum, Magic Eye, Waiting Room, Breakthrough, and Amnesia), many pictures to illustrate the various levels as well as the particular emergent geometries, and a theoretical discussion of the various algorithmic reductions that might explain how the hyperbolization of phenomenal space takes place based on combining a series of simpler effects together.
From another article on the same website - Algorithmic Reduction of Psychedelic States
Every acid head and psychedelic researcher has a pet theory of what these compounds are really doing in one’s mind. Many of these folk theories about the effects of psychedelics involve ontologies that currently have little scientific support (such as souls, thought fields, spirit worlds, archetypes, alien conspiracies, and so on). Although we cannot rule out explanations of this sort (talking about conventional explanations of DMT experiences) out of hand, the ontologies themselves are so abstract and poorly defined that we cannot accept them as useful forms of reductions. That said, their future versions will be more interesting. It is likely that committed, rational, spiritual psychedelic users will formalize models of this sort at some point. Rather than talking about a “spirit world,” they will talk about “mind-independent extra-dimensional space that consciousness can access in altered states” and then go on to define the differential equations that govern consciousness’s interactions with this space. When this happens, we will be in a much better position to assess the validity of these models, test the reality of those spaces, and perhaps even recruit the extra-dimensional inhabitants of these worlds for computational tasks.
Wanted to share in light of @ark's recent April 2022 Cassiopaean session discussion. Happy to hear your thoughts!
