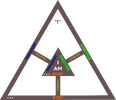
To add these are the two-arm paths (1→0→5→3→2) & (3→0→5→1→2) that bear stricking similarity to the Svastika if represented in a 2D symbol. Also, notice the of the 10 possible node pairs (including the centroid)
Also, more detail to this progression, as a geometric topology, surfaces (faces) are distinct functions, and we could say, recursive patterns stemming from the first 4 points (0,1,3). This lead me to consider that 4-7 correspond to the faces and in Kabalistic terms - the 4 worlds. So if follow this through, symbolically at least, we have:
- "Day 0": Point: Fire (0) - inhale
- Day 1: Line: Air (1) - exhale
- Day 2: Surface: Water (2) - inhale
- Day 3: Volume: Earth (3) - exhale
- Day 4: Face 1: Fire (0,1,2) - Atziluth (emmanation) - inhale
- Day 5: Face 2: Air (0,1,3) - Beriah (creation) - exhale
- Day 6: Face 3: Water (0,2,3) - Yetzirah (formation) - inhale
- Day 7: Face 4: Earth (1,2,3) - Assiah (action) - exhale
View attachment 110552
Image above depicts how each "world" has a breath function too. This is further reiterated via next key events / function in Genesis: Tree of Knowledge and Tree of Life (inhale and exhale). So a decent into knowledge (1→0→5→1→0 fire and air) burns when not balanced with the exhale in life (3→0→5→1→2). We see that same metaphor in the Ark of the Covenant and the Holy Grail. In other words, truth without care, law without grace, structure without flow - is incomplete and casts us out of the garden of Eden.
Consider again the burning bush - it ignites without being extinguished, the breath YHWH that is fully "breathing". This is the complete 10 progressions (Decad / Tetraktys):
9. "Day 8": Arm 1 (Svastika): Fire and Air - via 4 connections - inhale (decent of strain to centroid - the 5th node / 5th element / Adam Kadman / Aether)
10: "Day 9": Arm 2 (Svastika): Water and Earth - via 4 connections - exhale (release of novelty from centroid)
This traces the 10 possible node pairs via this "breath cycle". Given both trees are fall on progression 9 and 10 (day 8 & 9) these "branches" might just be the 10 Sephira. But two of those remain "untraced". These are node pairs 1-3 (a double inhale) and 0-2 (a double exhale). Perhaps they are Keter - a crown (above head/body) - sometimes said to be "Ayin" - nothing. And Yesod - the foundation and transparency of transmission. Serving here more of "silent" function?
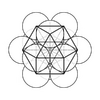
So back to the idea of the star tetrahedron. If the first tetrahedron is something like the most basic topology / consciousness unit / monad, then a mirror / shadow / polarity completes it (as above so below; STO/STS; action and equal and opposite reaction; peak is balanced by a trough, heartbeat and breath itself etc.). This provides then an additional 10 progressions across all nodes, faces and connections "sephira") (via 6 edges + 4 to centroid):
View attachment 110553
As you can see this foms the 3-4-3-4 cuboctahedron, an Archimedean solid, also known as ‘vector equilibrium’ coined by Buckmister Fuller. He called that the zero starting point for happenings or nonhappenings.. "it is the empty theater and empty circus and empty Universe ready to accommodate any act and any audience". This describes how the "centroid" (Aether, Adam Kadman etc.) is no actually a point but a non-local, 4th dimensional geometry. So the "breath cycle only ever moves towards the centre but never full entering it.
The star tetrahedron also forms a cube. This provides a cubic boundary of 6 new faces and x,y,z directional space + growth vectors (inhale and exhale): up, down, left, right, forward, back If we follow the inhale/exhale it transpires as follows:
...11-20 (day 10-19) the phases of the mirror tetrahedron: from Kaf (כ) to Resh (ר) that ends with an "exhale"
21. Shin (ש): Up
22. Tav (ת): Down
23. Kaf Sofit (ך): Left
24. Mem Sofit (ם): Right
25. Nun Sofit (ן): Forward
26. Pe Sofit (ף): Back
27. Tsade Sofit (ץ): Seed growth in 6 directions.
There's a bunch of other fascinating connections that seem to unravel from this too. Will add more.