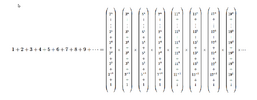
What does that mean? Is it mathematics? Or is it a poetic expression? If it is mathematics, I do not know such a concept as "infinite continuation". What would it mean that two "infinite continuations are equal? Is 1+1+1 ... = 1+2+3.... true? When two differently looking infinite continuations are supposed to be related by the "=" symbol?The infinite continuation of a specific sum series. I am assuming the exclamation point is a typo. I could be wrong?
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
christx11
Jedi Master
I understand what you are saying. I just don't understand where you are saying I am doing what you refer to.What does that mean? Is it mathematics? Or is it a poetic expression? If it is mathematics, I do not know such a concept as "infinite continuation". What would it mean that two "infinite continuations are equal? Is 1+1+1 ... = 1+2+3.... true? When two differently looking infinite continuations are supposed to be related by the "=" symbol?
Are you saying for example:
x = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ...
Are you saying the right hand side of the above ( the sum series of all natural numbers),
Are you saying the right hand side cannot be re-written as two infinite sum series as the evens plus the odds?
As in:
x = ( 2 + 4 + 6 + 8 + 10 + 12 +14 + ... ) + ( 1 + 3 + 5 + 7 + 9 +11 +13 + ... )
Are you saying that the sum of the odds plus the sum of the evens is not the sum of all natural numbers?
Or, more exactly, what the equal sign "=" between two such formal expressions means for you.I am saying that I do not know the concept of "infinite sum series". Please define the concept for me. Or give a link. I can't find it online.
In your case both sides are divergent. They produce both infinity. What do you mean by the fact that the two infinities are "equal"?
You probably mean (I am guessing), that with an appropriate procedure on the right hand side (infinite product) you can recover the elements of the left hand side one-by-one? Is that what you mean? Not only "elements" but also partial sums. Is this the case?Or, more exactly, what the equal sign "=" between two such formal expressions means for you.
In your case both sides are divergent. They produce both infinity. What do you mean by the fact that the two infinities are "equal"?
christx11
Jedi Master
You are right Ark. I will try to clean up the nonsense statements like 'infinite sum series', it really makes a mess of everything.You probably mean (I am guessing), that with an appropriate procedure on the right hand side (infinite product) you can recover the elements of the left hand side one-by-one? Is that what you mean? Not only "elements" but also partial sums. Is this the case?
I need to go back to something much more simple and basic. None of what I am trying to show involves calculus. Everything I am trying to demonstrate is historically from publicly available mathematics that existed 1900 years before calculus was even discovered. None of it requires convergence, divergence, limits, partial sums, etc.
To continue my thought experiment requires a starting point that the entire set of natural numbers (expressed as an infinite series) and the entire set of rational numbers (expressed as an infinite series), each have an equality as an infinite product, where each term of the infinite product is a prime geometric series.
1) We know that the infinite series of all inverse natural numbers can be expressed as an infinite product, where each term of the infinite product is a prime geometric series. (Euler's Theorem 7)
2) I will provide the data and logic to demonstrate that a similar equality exists for the natural numbers. That the infinite series of all natural numbers can also be expressed as an infinite product, where each term of the infinite product is a prime geometric series.
3) I will provide the data and logic to demonstrate that a similar equality exists for the rational numbers. That the infinite series of all rational numbers can also be expressed as an infinite product, where each term of the infinite product is a prime geometric series.
*** Note in the above image: "the sum of all rationals", should be "the infinite series of all rational numbers"
Numbers 2 and 3 above I do not think can be proven algebraically. None the less, I think both are true, and the data and logic simply goes back to the sieve of Eratosthenes. The sieve of Eratosthenes has much more information in it than it just being a way to find prime numbers.
I will put the relevant information together and post here. It may take me a while (Jan 2025, maybe sooner).
Interestingly the data and logic from the sieve of Eratosthenes, Ark has already mentioned in a blog post here.
The link Ark mentions is: A periodic table of primes: Research team claims that prime numbers can be predicted
The actual paper is at The Periodic Table of Primes
You can see from one of the links above it is mentioned as a breakthrough-prime-theory...
It is a breakthrough except, James McCanney made this same breakthrough discovery here:
James McCanney
New Definition of Prime Numbers with Sppn Tables and Proofs by Induction
Except Liu Fengsui, made the same breakthrough discovery here:
Liu Fengsui's Prime Formula Problem 37. The Liu Fengsui's Prime Formula
Except Gary Croft made the same breakthrough discovery here: 'The Prime Spiral Sieve' Prime Numbers Demystified by 8-Dimensional Algorithms
And the information that all of the above parties are seeing (breakthrough discovery), is simply already found in the fine details of the information already available over 2000 years ago in the sieve of Eratosthenes.
And it is that same information from the sieve of Eratosthenes, that is the logic and data needed to prove:
2) That the infinite series of all natural numbers can also be expressed as an infinite product, where each term of the infinite product is a prime geometric series.
3) That the infinite series of all rational numbers can also be expressed as an infinite product, where each term of the infinite product is a prime geometric series.
Coincidentally, the same information (data and logic from the sieve of Eratosthenes) appears in Euler's theorem 7.
Attachments
christx11
Jedi Master
Here is the logic for the proposition that all 3 sets of numbers ( inverse naturals, naturals, and rationals ) have equalities where the infinite series of each set can be expressed as an infinite product where each term of the infinite product is a prime geometric series.
There is no calculus. Just simple addition and multiplication.
I have created posts on my blog explaining the additional data in the 'Sieve of Eratosthenes' that leads to my conclusions.
The Sieve of Eratosthenes - Backing Up

 timefree.blogspot.com
timefree.blogspot.com
The 'The Sieve of Eratosthenes - Part 2
 timefree.blogspot.com
timefree.blogspot.com
There is no calculus. Just simple addition and multiplication.
I have created posts on my blog explaining the additional data in the 'Sieve of Eratosthenes' that leads to my conclusions.
The Sieve of Eratosthenes - Backing Up
The Sieve of Eratosthenes - Backing Up
Math, Extraordinary claims, Extraordinary evidence
The 'The Sieve of Eratosthenes - Part 2
The 'The Sieve of Eratosthenes - Part 2
Math, Extraordinary claims, Extraordinary evidence
PabloAngello
Jedi Master
I have a feeling this interview somewhat fits this thread:
"Christopher Michael Langan (born March 25, 1952) is an American horse rancher and former bar bouncer, known for scoring highly on an IQ test that gained him entry to a high IQ society, and for being formerly listed in the Guinness Book of Records high IQ section."
SasaM
Dagobah Resident
Regarding the information flow, perhaps it might be useful to consider that most probably nothing in nature ever happens in veritable vacuum. Wherever we looked, we observed some background field, in most general case a rotating cosmic EM fields, even when particle densities were considered infinitesimally small. Using that observation as a sort of analogy also for most probably rotating cosmic information field, as the Universe observes itself, we then might conclude that at a certain depth level in the field, the information transfer would naturally, due to in effect kind of Coriolis and shear stress forces and sort of a drag, flow in opposite direction compared to the direction just below or near the surface.
On smaller scales that's observed with so called wind induced "horizontal" sea currents, and modeled in simple way by so called Ekman spiral (Wikipedia link).

Tentatively, this observed phenomenon and its mathematical model, might even provide analogy for how natural communication between different densities, as levels or sort of layers of different density in the probably rotating cosmic information field occurs. Kind of providing a possible explanation or mechanism, or just part of it, why we usually refer to souls, as a sort of our 5D selves, perceiving what we usually see in everyday lives in a kind of reversed or upside down fashion. Also, it might suggest a mechanism for establishing sort of a natural feedback loop between observer and observed, for example when communication or information transfer happens during an observation.
In a more practical, down to Earth way, if we take into account the scaling difference in density and it's gradient, we also come to a natural simple addition to EM effects presented in ECHCC for possible explanations for spiraling phenomena in the Earth's atmosphere, like tornadoes and hurricanes and cyclones etc. Since in the atmosphere density decreases with height, and it changes on much larger scale, in addition to scaling difference in its value, density of air to density of water roughly as 1:1000, if we look from upside down stance, the Ekman spiral model would suggest sort of an enlarging spiraling transport going from the surface up, towards higher altitudes in the atmosphere, just like the waterspouts for example appear to us standing on the surface.
FWIW.
On smaller scales that's observed with so called wind induced "horizontal" sea currents, and modeled in simple way by so called Ekman spiral (Wikipedia link).
The Ekman spiral is an arrangement of ocean currents: the directions of horizontal current appear to twist as the depth changes. The oceanic wind driven Ekman spiral is the result of a force balance created by a shear stress force, Coriolis force and the water drag. This force balance gives a resulting current of the water different from the winds. In the ocean, there are two places where the Ekman spiral can be observed. At the surface of the ocean, the shear stress force corresponds with the wind stress force. At the bottom of the ocean, the shear stress force is created by friction with the ocean floor. This phenomenon was first observed at the surface by the Norwegian oceanographer Fridtjof Nansen during his Fram expedition. He noticed that icebergs did not drift in the same direction as the wind. His student, the Swedish oceanographer Vagn Walfrid Ekman, was the first person to physically explain this process.

Tentatively, this observed phenomenon and its mathematical model, might even provide analogy for how natural communication between different densities, as levels or sort of layers of different density in the probably rotating cosmic information field occurs. Kind of providing a possible explanation or mechanism, or just part of it, why we usually refer to souls, as a sort of our 5D selves, perceiving what we usually see in everyday lives in a kind of reversed or upside down fashion. Also, it might suggest a mechanism for establishing sort of a natural feedback loop between observer and observed, for example when communication or information transfer happens during an observation.
In a more practical, down to Earth way, if we take into account the scaling difference in density and it's gradient, we also come to a natural simple addition to EM effects presented in ECHCC for possible explanations for spiraling phenomena in the Earth's atmosphere, like tornadoes and hurricanes and cyclones etc. Since in the atmosphere density decreases with height, and it changes on much larger scale, in addition to scaling difference in its value, density of air to density of water roughly as 1:1000, if we look from upside down stance, the Ekman spiral model would suggest sort of an enlarging spiraling transport going from the surface up, towards higher altitudes in the atmosphere, just like the waterspouts for example appear to us standing on the surface.
FWIW.
palestine
Dagobah Resident
@christx11, I have been reading your posts with a great interest, because I sometimes do some algebra in order to keep the mind stable. I wanted to ask you a couple of questions about algebra work / maths.Here is the logic for the proposition that all 3 sets of numbers ( inverse naturals, naturals, and rationals ) have equalities where the infinite series of each set can be expressed as an infinite product where each term of the infinite product is a prime geometric series.
There is no calculus. Just simple addition and multiplication.
I have created posts on my blog explaining the additional data in the 'Sieve of Eratosthenes' that leads to my conclusions.
The Sieve of Eratosthenes - Backing Up

The Sieve of Eratosthenes - Backing Up
Math, Extraordinary claims, Extraordinary evidencetimefree.blogspot.com
The 'The Sieve of Eratosthenes - Part 2
The 'The Sieve of Eratosthenes - Part 2
Math, Extraordinary claims, Extraordinary evidencetimefree.blogspot.com
I think that the C's hinted at the study of basic algebra/math as positive. I would like to ask you about the "bridge" that math allows. I am having hard times than to translate how algebra/math could be useful. Well, more technically, I am not able to bridge any form of "cosmical knowledge" after having been doing algebra.
I understand of course that it has to do with "information theory"; "intelligent design", and how the information channels are relating to prime/basic geometrical shapes (for example).
Pierre Lescaudron, for example, has been developping a model hinting at biophoton emissions - akin to generic geometric bits of light. That's not exactly what he said but I hope that you get my point. And so, from there, I would understand that algebra/math are hinting at the basic fabric of the Universe, especially in regard of information structure. When we think, when we learn, it's about geometrical prime structures which are undergoing some "motions", so to speak. Pierre hinted at the Information Field, and so it would represent a potential factor to take in consideration, in addition to the basic motion of "geometrical shapes".
I am having hard time, thus, to be able to bind algebra with any form of further study. The above is my naive understanding of it but I wish, one day, than to be able to work more deeply on those matters. Would you have any suggestion? How do you "see things" or would explain/teach others in terms of "algebra/math >>> an objective cosmological model"? It seems to me that this is more or less what mathematicians would be aiming for.
I don't find your pics complicated; except for a few hints that you provided, I am having hard times seeing where you would be headed, after the theory is validated (it remained at some pure math level: how would you use your findings?). You surely have an idea but I could not see what would be "the next step"
 I am sure that you, yourself, see the next "stage" - and I would be very happy to understand, then, how a mathematician would proceed! Thank you for any lights on this spec!
I am sure that you, yourself, see the next "stage" - and I would be very happy to understand, then, how a mathematician would proceed! Thank you for any lights on this spec!If you don't have the time (or for another reason), that's okay. Any way this is fascinating! I was thinking if we could set up some basic algebra class rooms! Doing math puts the brain back to 1+1=2 and I found it very useful during chaotic times, with a lot of nonsense. It helps the mind to remain structured, and provides an additional logical and sane structure.
SasaM
Dagobah Resident
Regarding the DNA as an information storage and possibly an antenna which enables the connection with the cosmic information field, it might be handy to have its visual representation in a geometrical sense.
A short and seemingly easy to digest text about the geometry of the DNA can be found on this link, where the DNA double helix is illustrated by the following image (maybe turn on the Light mode for the text to appear more clearly, as well as for some of the next images in the post).

A helix (Wikipedia link) is generally considered as a geometrical three-dimensional spiral.

On another Wikipedia entry (link), we find that the central projection of a helix onto a plane perpendicular to the axis of the helix describes the view that one would see of the guardrail of a spiral staircase, looking up or down from a viewpoint on the axis of the staircase.

Mathematically, that is geometrically, the central projection of a helix describes a hyperbolic or reciprocal spiral (Wikipedia link).

Apart as the central projections of helixes, hyperbolic spirals can also be generated as the inverse curves of Archimedean spirals (Wikipedia link).

Since a nice "draw it yourself" image or an approximation of the Archimedean spiral is the Pythagorean spiral (Wikipedia link), we came to a possible visual representation of the DNA as our informational link to Reality.
In similar fashion as shortly discussed in previous post here, the graphic representation shown below works in an inside out manner, like viewing the double helix from its center outwards, or in sort of inverted way meaning that the two connected Pythagorean spirals expand as they go on with their (un)winding. The connecting links or so called ladders in the DNA double helix are represented in the image by the pairs of corresponding square root lines.

FWIW.
A short and seemingly easy to digest text about the geometry of the DNA can be found on this link, where the DNA double helix is illustrated by the following image (maybe turn on the Light mode for the text to appear more clearly, as well as for some of the next images in the post).

A helix (Wikipedia link) is generally considered as a geometrical three-dimensional spiral.
On another Wikipedia entry (link), we find that the central projection of a helix onto a plane perpendicular to the axis of the helix describes the view that one would see of the guardrail of a spiral staircase, looking up or down from a viewpoint on the axis of the staircase.

Mathematically, that is geometrically, the central projection of a helix describes a hyperbolic or reciprocal spiral (Wikipedia link).
Apart as the central projections of helixes, hyperbolic spirals can also be generated as the inverse curves of Archimedean spirals (Wikipedia link).
Hyperbolic spiral (blue) as image of an Archimedean spiral (green) by inversion through a circle (red)
Since a nice "draw it yourself" image or an approximation of the Archimedean spiral is the Pythagorean spiral (Wikipedia link), we came to a possible visual representation of the DNA as our informational link to Reality.
In similar fashion as shortly discussed in previous post here, the graphic representation shown below works in an inside out manner, like viewing the double helix from its center outwards, or in sort of inverted way meaning that the two connected Pythagorean spirals expand as they go on with their (un)winding. The connecting links or so called ladders in the DNA double helix are represented in the image by the pairs of corresponding square root lines.
FWIW.
christx11
Jedi Master
@christx11, I have been reading your posts with a great interest, because I sometimes do some algebra in order to keep the mind stable. I wanted to ask you a couple of questions about algebra work / maths.
I think that the C's hinted at the study of basic algebra/math as positive. I would like to ask you about the "bridge" that math allows. I am having hard times than to translate how algebra/math could be useful. Well, more technically, I am not able to bridge any form of "cosmical knowledge" after having been doing algebra.
I am having hard time, thus, to be able to bind algebra with any form of further study. The above is my naive understanding of it but I wish, one day, than to be able to work more deeply on those matters. Would you have any suggestion? How do you "see things" or would explain/teach others in terms of "algebra/math >>> an objective cosmological model"? It seems to me that this is more or less what mathematicians would be aiming for.
I don't find your pics complicated; except for a few hints that you provided, I am having hard times seeing where you would be headed, after the theory is validated (it remained at some pure math level: how would you use your findings?). You surely have an idea but I could not see what would be "the next step"I am sure that you, yourself, see the next "stage" - and I would be very happy to understand, then, how a mathematician would proceed! Thank you for any lights on this spec!
My basic idea is that by changing one very limited definition, something very much like what the C's sessions describes as the densities becomes apparent.
I think the densities are simple, I think they are fundamental and I think they are sets. The following two C's session quotes are very much related.
Session 18 July 1998
Q: (A) Can we have a UFT which unifies EM and gravity and does not include the concept of other densities. In other words, can we put in a textbook all about the gravity and electromagnetics, and a student could learn all of this and still know nothing about other densities?
A: No. Other densities become apparent when...
Session 10 July 1999
A: Gravity is the binder.
Q: (A) But, my question is: gravity is a term that is defined in dictionaries and encyclopedias and is a term which has a very precise meaning for physicists and mathematicians. I want to know if you are talking about the same thing or if you are using the term 'gravity' to describe something completely different that we know as gravity. Are we talking about the same thing?
A: Well, are you certain these "definitions" you speak of are not limited?
Q: (A) Yes, I am sure they are limited. Nevertheless, they are precisely defined concepts and you are using the same term 'gravity,' so I am asking if we are talking about the same thing, or if you are talking about something completely different?
A: How about a great expansion upon the same concept?
I think the "Other densities become apparent when...", when we drop one very limited definition that only allows us to see that which we wish to see.
The information on the Sieve of Eratosthenes is to hopefully show that all three sets (inverse naturals, naturals, and rationals) all have equalities where their infinite series is equal to an infinite product expression where each term of the infinite product is a prime geometric series. I consider the infinite product expression(s) for each set where each term of the infinite product is a prime geometric series is probably the most important expression in mathematics next to the prime numbers themselves.
I consider the infinite product expression(s) not just as equal to the sets infinite series expression, but that the infinite product expression actually generates the infinite series expression. Performing every operation in the infinite product expression (every addition and every multiplication) actually creates the infinite series. But when I perform all of the operations I actually get two infinite series created by the infinite product expression(s). One series is the regular series we normally equate with the infinite product (example: the infinite product expression for the inverse natural numbers generates the harmonic series), but a second parallel series is also generated where every term of the series has countably infinite factors. Mathematics says this second set does not exist.
Here is the image of the series of all inverse natural numbers equal to its infinite product expression where each term of the infinite product is a prime geometric series.
Figure 1
I am making the claim that the infinite product expression on the right hand side also generates a second infinite series, synchronously/simultaneously, where every term of the infinite series has infinite factors. Something like this:
Not only am I claiming that a second series where each term has infinite factors is created, but the terms of that series are a set where all elements of the set have countably infinite factors and if we assume something like the transfer principle, then these numbers are orderable and are closed under addition and multiplication and both have the number 1 as their first member which is the multiplicative identify in both sets. The first member of the set is 1. I also claim that one half of all the numbers generated by the infinite product have finite factors and one half of all numbers generated by the infinite product have infinite factors. I am also claiming that the simultaneous creation of both sets of numbers is such that a2 behaves as the prime number 2 does in the finitely factored set, a3 behaves as the prime number 3 does in the finitely factored set, just as 4 is 2 squared in the finitely factored set, a4 is a22 in the infinitely factored set. Yes, I am claiming something like infinitely factored prime numbers. This leads to the idea that this second set of infinitely factored inverse natural numbers also has an infinite product expression like the following:
Figure 2
I am claiming that this same logic exists in all three set scopes (inverse natural numbers, natural numbers, and rational numbers) and that these are the first three densities.
To explicate that a little further, I can demonstrate the idea with current limited definitions from mathematics.
| Set Scope | Representation | Constraint |
| Any natural number can be uniquely represented as an infinite product taken over all the prime numbers, as | where a finite number of the ni are positive integers, and the others are zero. | |
| Any inverse natural number can be uniquely represented as an infinite product taken over all the prime numbers, as | where a finite number of the ni are negative integers, and the others are zero. | |
| Any rational number can be uniquely represented as an infinite product taken over all the prime numbers, as | where a finite number of the ni are positive or negative integers, and the others are zero. |
In each of the above three definitions, why is the third part of the definition (Constraint) where it says a finite number of exponents are not zero and all the rest must be zero, why is that necessary?
That question is both rhetorical and serious. I understand that in the scope of each of the three sets, all elements of the set are finite numbers (finitely factored). But at the same time that tells us something else. It tells us that with countably infinite prime numbers as terms to create a number, and with each prime number term having as possibilities for exponents the respective scope of exponents, that if we do not limit the number of terms that can have non-zero exponents, we will create a number not in the respective set. It is an admission to the fact that countably infinite prime numbers, each with their respective selection of exponents can create numbers that have infinite factors. In fact we can modify the last part of the definition and change it from "where a finite number of the ni are negative integers" to "where an infinite number of the ni are negative integers". In this case the definitions will create only infinitely factored numbers and no finitely factored numbers. Better yet, we can drop the part of the constraint that talks about how many terms can have non-zero exponent values entirely and this will allow both finitely factored and infinitely factored numbers to be created simultaneously.
What are these other numbers? How many of them are there? Shouldn't I be able to open a text on fundamental number theory and somewhere in the first 3-5 chapters where it talks about sets and the fundamental theorem of arithmetic and factorization, shouldn't it mention these other numbers and sets in the text somewhere? Mathematics does not even admit that they exist. Are these definitions allowing us to see only what we wish to see (finitely factored numbers)? Are these definitions preventing us from seeing objectively?
Within this idea also arises the idea of gravity as a binder, and "a great expansion upon the same concept" as we use the concept.
The idea of gravity can be demonstrated with any of the levels/densities. I will use level 3, the rationals, to show it.
Figure 3 ( The infinite product expression that is equal to the infinite series of all rational numbers )
The above expression creates/generates the infinite series of all rational numbers. It also creates/generates an infinite series of all infinitely factored rational numbers.
So, what happens if we remove a single term of the infinite product, a single prime geometric series term? For instance the prime number 2 geometric series.
What happens is that every number divisible by the number 2 disappears from the finitely factored rationals series and every number divisible by 2 disappears from the infinitely factored rationals series. Poof they are gone from both series. If we put the the the prime number 2 geometric series term back in the expression, boom, all numbers divisible by 2 re-appear in both series. The two sets (with finitely factored and infinitely factored elements) are bound together by the prime geometric series. One cannot exist without the other. Yes, connected, intertwined, bonded... Merged. Perfect balance. I realize I am mixing sets terminology here with series terminology. The generated finitely factored series implies the existence of the finitely factored set (the regular rationals), and the generated infinitely factored series implies the existence of the set of rationals where every element is infinitely factored and neither set can exist without the other.
And how is a prime geometric series in anyway related to the concept we call gravity and is a great expansion on that concept? One of the most famous properties of what we call gravity is the inverse square law. I can't think of a greater expansion on the idea of inverse square than the entire geometric series, instead of just a single element - inverse square.
So what is the 4th level, 4th density? The third density is the finitely factored set of rationals and its parallel infinitely factored set of rationals. This is the first level where we have a true field, the rationals, and the parallel infinitely factored rationals field. The finitely factored field if I understand properly is Archimedean and the infinitely factored field is non-Archimedean. There are also a couple of properties I think that popup from third density.
3rd Density property 1:
---------------------------
Each term of the infinite product expression (a prime geometric series) has a square range.
What do I mean? The 2 prime geometric series, for any exponent there is an inverse exponent. The distance between the two is square.
Example: The distance from 210 to 2-10 is 220.
In fact the distance between 2n and 2-n for any integer n, is 22n.
The range is square to every infinite n exponent. A perfectly square nature.
And if each term has a square range, then the range of the entire infinite product expression is:
22n x 32n x 52n x 72n x ... = (2 x 3 x 5 x 7 x ...)2n
The entire infinite product expression has a perfectly square nature.
The geometric object that I know of that is perfectly square, is a plane.
---------------------------
3rd Density property 2:
---------------------------
Each prime geometric series is a loop.
What do I mean?
Each prime geometric series has an infinity in two directions.
The positive integer exponent keeps growing larger and larger to infinity. There is no upper bounded integer exponent.
The negative integer exponent keeps growing smaller and smaller to infinity (approaching zero). There is no lower bounded integer exponent.
I propose this could be a loop similar in the way that in thermo-dynamics it is proposed that the highest temperature possible is anything below absolute zero, the highest and lowest temperatures possible wrap around in a loop.
---------------------------
If these properties are possible, then it is possible that the infinite product expression geometrically is a cylinder.
Forth level / density builds on third density by implementing Euclid's idea of introducing a real valued variable into the exponent (as in Eulcid's zeta function), but here we implement the real valued variable over the rationals and not just the inverse naturals as Euclid did.
This results in an infinite product that looks like:
Figure 4 (Infinite product expression for 4th density)
For each real value of s, there is a unique/distinct infinite product, which creates a unique/distinct finitely factored series and a parallel unique/distinct infinitely factored series. Which implies for each real value of s, there is a unique/distinct finitely factored Archimedean set and a parallel unique/distinct infinitely factored non-Archimedean set.
Fourth density is like a field of fields. Because there are uncountably infinite values for the real valued variable s, there are uncountably infinite pairs of Archimedean and non-Archimedean fields as in a continuum. You can look at each value of s as a slice that creates a unique/distinct Archimedean and non-Archimedean pair of fields.
The real valued variable s, also introduces the possibility of a much larger second loop like structure geometrically, as the reals also have property 2 and property 3 of third density and this may curve the cylinder of third density into a torus.
I believe the Archimedean fields have a space like metric and the parallel infinitely factored non-Archimedean field metric is ???
Fifth and Sixth level / densities
5th and 6th densities simply build on 4th density. 4th, 5th, and 6th have a similar profile. In fact 5th and 6th are achieved simply by using the same infinite product expression of 4th density and expanding the real valued variable s to include all of the infinitely factored numbers that are extant from all of the infinitely factored parallel sets. This would be like expanding the infinitely factored variable s to include something like the hyper-reals and the surreals.
In fourth density the finitely factored sets have numbers where every number has a finitely factored base and a finitely factored exponent. In fourth density the infinitely factored parallel sets have numbers where every number has an infinitely factored base and a finitely factored exponent.
When we expand the real valued variable s to all infinitely factored numbers, what were finitely factored numbers with finitely factored bases and finitely factored exponents of 4th density now have finitely factored bases with infinitely factored exponents, every number is now infinite. This is fifth density.
The parallel infinitely factored numbers of 4th density, where each number had an infinitely factored base and a finitely factored exponent now have infinitely factored bases and infinitely factored exponents. This is 6th density.
5th and 6th density are bound together also by gravity (the prime geometric series), neither can exist without the other.
That's it.
I equate the finitely factored sets as space like and the parallel infinitely factored sets to be??? not-space-like, maybe energy or consciousness or both. The first four levels/densities are one-half space-like and one-half not-space-like. Densities 4 through sixth have the same profile by the introduction of the variable in the exponent and the possible double loop of the cylinder.
I think these are the densities. I think this is what the secret scientific intelligence matrix has known about for some 60 to 80 years. The information in itself is not dangerous at all. But they have spent 60 to 80 years developing new mathematics around this new paradigm and it is the new mathematics and applying it to new physics and new weapons, etc. that is dangerous.
Here is a very simplistic diagram of the current paradigm:
Current Math/Science paradigm / world view (1)
All of mathematics, science and engineering comes out of this current paradigm. The cloud at the top contains thousands of more entries. I just put a few in.
The new paradigm (2) and new math should be built on this.
This all arises once we un-limit a couple of very limited definitions that tell us prime numbers can only create finitely factored numbers and we quit seeing only what we wish to see.
I know I don't always use the proper terminology. But I am pretty sure of what I see and I am trying my best to communicate that.
I think the missing link that the C's sessions said was earlier in the mathematical process is paradigm 2. What could be earlier in the process than the fundamental foundations of arithmetic? I think the fundamental foundations of arithmetic in paradigm (1) is true, but it is a half truth. I think the fundamental foundations of arithmetic in paradigm (2) is the objective reality.
I think Ark is in that cloud of paradigm (1). I am sure there are thousands of useful things that have arisen in paradigm (1) that apply to and are useful to paradigm (2), but paradigm (2) probably requires a whole lot of new mathematics also.
I think under paradigm (2), that dozens of the C's session answers about science and math begin to make sense. There are literally dozens of them.
Here are a couple of C's session quotes. Not the most astonishing that apply to paradigm (2), but interesting none the less.
=========================================
Session 22 July 2000
=========================================
The "trick" that 3rd density STS life forms will learn, either prior to transition to 4th density, or at the exact juncture, is to think in absolutely limitless terms.
=========================================
This C's excerpt is more like a prophecy, "think in absolutely limitless terms". Limitless terms (infinitely factored numbers).
=========================================
Session 13 June 1998
=========================================
A: You must remember mosaic, matrix... When you are on the verge of quantum changes or discovery, the realities begin to reveal their perfectly squared nature to you.
=========================================
Session 18 July 1998
=========================================
Q: (T) Fourth density. (A) We were told earlier that this UFT opens the door to other densities...
A: Yes.
Q: (A) And, some time ago Santilli was here and he had his own idea about UFT; gravity and anti-gravity, and he was told that he had a good idea of UFT, but that he only has one seventh of the equation. I don't understand why UFT has to go to other densities? Does it follow, or is it necessary once we have UFT, that the other densities will become clear in that they are necessary? How is it?
A: Fragmented inquiry.
Q: (A) Can we have a UFT which unifies EM and gravity and does not include the concept of other densities. In other words, can we put in a textbook all about the gravity and electromagnetics, and a student could learn all of this and still know nothing about other densities?
A: No. Other densities become apparent when...
=========================================
Session 10 July 1999
=========================================
Q: (A) Okay, no clue there. Now, next question relates to the story of creation which L wrote for the website, and I was reading it and trying to make sense, to make it not contradictory, and I found that it is not easy because many of the concepts that are used during these sessions are somehow contradictory to each other or they don't quite fit with the standard meanings of these concepts, so I wanted to ask for some explanation. First, we were told that gravity is essentially the most universal force and that it is from this that everything originates...
A: Gravity is the binder.
Q: (A) But, my question is: gravity is a term that is defined in dictionaries and encyclopedias and is a term which has a very precise meaning for physicists and mathematicians. I want to know if you are talking about the same thing or if you are using the term 'gravity' to describe something completely different that we know as gravity. Are we talking about the same thing?
A: Well, are you certain these "definitions" you speak of are not limited?
Q: (A) Yes, I am sure they are limited. Nevertheless, they are precisely defined concepts and you are using the same term 'gravity,' so I am asking if we are talking about the same thing, or if you are talking about something completely different?
A: How about a great expansion upon the same concept?
=========================================
Session 4 January 1997
=========================================
A: Please... we are drifting! Tell A that "aether" is Terran material science's attempt to address ether. The trouble is, there is simply no way to physicalize a plane of existence which is composed entirely of consciousness. It is the union of perfect balance between the two "states" or planes, that is the foundation and essence of all creation/reality. You cannot have one without the other!
Q: (L) When you say the two states or planes, you are saying the physical state and the state of consciousness...
A: Yes.
Q: (L) And you can't have one without the other. And the state of consciousness and the state of material existence are so completely connected, that both are infinite? One cannot exist without the other...
A: Yes, connected, intertwined, bonded... Merged.
=========================================
There are dozens more C's excerpts that apply.
And I want to mention just one quote from a forum thread about 'Krzysztof Jackowski - Polish Clairvoyant'. I know so much of the prophecy stuff is just nonsense, but sometimes they pickup on something. It seems as if the forum has a lot of activity regarding prophecy and AI threads recently.
'Krzysztof Jackowski - Polish Clairvoyant'.
=========================================
Schwab - Jan 20, 2023
=========================================
"Benetta"… I don't quite understand what I'm going to say, but he belongs to some "Benetta Club". The first sentence that came to mind. In criminal matters, too, I have a sense of things I don't understand, and I say them. The essence of the matter is to reach the missing person, the body, or the living person. You have to say or write down aloud what comes to mind.
There is an elite club. No more than 15 people belong to this association. Or maybe it's a group of 15 people. It's called "Benetta". I have absolutely no idea what that means.
[He Googles "Benetta", but couldn't find anything sensible]
He is an intermediary. He doesn't belong to this club. He is like an ideological intermediary, a connection. As if these 15 people did not want to reveal themselves or be politically active. We have this forum in Davos, he can go there, but no one from this club will go there. I do not claim that he is the only intermediary, there may be more of them...
Strange... Something is going wrong in his opinion and he fears that people may be awakening prematurely. "Logo Arithmetica". What is happening in the world right now, I'm not talking about Ukraine, but other things, it's also about people, this is the "Logo Arithmetica". Something is going wrong with it, and he's afraid of waking people up too soon.
=========================================
Attachments
christx11
Jedi Master
Replying to my own post. The above should be Euler, not Euclid.Forth level / density builds on third density by implementing Euclid's idea of introducing a real valued variable into the exponent (as in Eulcid's zeta function), but here we implement the real valued variable over the rationals and not just the inverse naturals as Euclid did.
Forth level / density builds on third density by implementing Euler's idea of introducing a real valued variable into the exponent (as in Euler's zeta function), but here we implement the real valued variable over the rationals and not just the inverse naturals as Euler did.
Sol Logos
The Living Force
My basic idea is that by changing one very limited definition, something very much like what the C's sessions describes as the densities becomes apparent.
I think the densities are simple, I think they are fundamental and I think they are sets. The following two C's session quotes are very much related.
I think the "Other densities become apparent when...", when we drop one very limited definition that only allows us to see that which we wish to see.
The information on the Sieve of Eratosthenes is to hopefully show that all three sets (inverse naturals, naturals, and rationals) all have equalities where their infinite series is equal to an infinite product expression where each term of the infinite product is a prime geometric series. I consider the infinite product expression(s) for each set where each term of the infinite product is a prime geometric series is probably the most important expression in mathematics next to the prime numbers themselves.
I consider the infinite product expression(s) not just as equal to the sets infinite series expression, but that the infinite product expression actually generates the infinite series expression. Performing every operation in the infinite product expression (every addition and every multiplication) actually creates the infinite series. But when I perform all of the operations I actually get two infinite series created by the infinite product expression(s). One series is the regular series we normally equate with the infinite product (example: the infinite product expression for the inverse natural numbers generates the harmonic series), but a second parallel series is also generated where every term of the series has countably infinite factors. Mathematics says this second set does not exist.
Here is the image of the series of all inverse natural numbers equal to its infinite product expression where each term of the infinite product is a prime geometric series.
Figure 1
View attachment 108123
I am making the claim that the infinite product expression on the right hand side also generates a second infinite series, synchronously/simultaneously, where every term of the infinite series has infinite factors. Something like this:
View attachment 108124
Not only am I claiming that a second series where each term has infinite factors is created, but the terms of that series are a set where all elements of the set have countably infinite factors and if we assume something like the transfer principle, then these numbers are orderable and are closed under addition and multiplication and both have the number 1 as their first member which is the multiplicative identify in both sets. The first member of the set is 1. I also claim that one half of all the numbers generated by the infinite product have finite factors and one half of all numbers generated by the infinite product have infinite factors. I am also claiming that the simultaneous creation of both sets of numbers is such that a2 behaves as the prime number 2 does in the finitely factored set, a3 behaves as the prime number 3 does in the finitely factored set, just as 4 is 2 squared in the finitely factored set, a4 is a22 in the infinitely factored set. Yes, I am claiming something like infinitely factored prime numbers. This leads to the idea that this second set of infinitely factored inverse natural numbers also has an infinite product expression like the following:
Figure 2
View attachment 108125
I am claiming that this same logic exists in all three set scopes (inverse natural numbers, natural numbers, and rational numbers) and that these are the first three densities.
To explicate that a little further, I can demonstrate the idea with current limited definitions from mathematics.
Set Scope Representation Constraint Any natural number can be uniquely represented as an infinite product taken over all the prime numbers, as View attachment 108119 where a finite number of the ni are positive integers, and the others are zero. Any inverse natural number can be uniquely represented as an infinite product taken over all the prime numbers, as View attachment 108119 where a finite number of the ni are negative integers, and the others are zero. Any rational number can be uniquely represented as an infinite product taken over all the prime numbers, as View attachment 108119 where a finite number of the ni are positive or negative integers, and the others are zero.
In each of the above three definitions, why is the third part of the definition (Constraint) where it says a finite number of exponents are not zero and all the rest must be zero, why is that necessary?
That question is both rhetorical and serious. I understand that in the scope of each of the three sets, all elements of the set are finite numbers (finitely factored). But at the same time that tells us something else. It tells us that with countably infinite prime numbers as terms to create a number, and with each prime number term having as possibilities for exponents the respective scope of exponents, that if we do not limit the number of terms that can have non-zero exponents, we will create a number not in the respective set. It is an admission to the fact that countably infinite prime numbers, each with their respective selection of exponents can create numbers that have infinite factors. In fact we can modify the last part of the definition and change it from "where a finite number of the ni are negative integers" to "where an infinite number of the ni are negative integers". In this case the definitions will create only infinitely factored numbers and no finitely factored numbers. Better yet, we can drop the part of the constraint that talks about how many terms can have non-zero exponent values entirely and this will allow both finitely factored and infinitely factored numbers to be created simultaneously.
What are these other numbers? How many of them are there? Shouldn't I be able to open a text on fundamental number theory and somewhere in the first 3-5 chapters where it talks about sets and the fundamental theorem of arithmetic and factorization, shouldn't it mention these other numbers and sets in the text somewhere? Mathematics does not even admit that they exist. Are these definitions allowing us to see only what we wish to see (finitely factored numbers)? Are these definitions preventing us from seeing objectively?
Within this idea also arises the idea of gravity as a binder, and "a great expansion upon the same concept" as we use the concept.
The idea of gravity can be demonstrated with any of the levels/densities. I will use level 3, the rationals, to show it.
Figure 3 ( The infinite product expression that is equal to the infinite series of all rational numbers )
View attachment 108130
The above expression creates/generates the infinite series of all rational numbers. It also creates/generates an infinite series of all infinitely factored rational numbers.
So, what happens if we remove a single term of the infinite product, a single prime geometric series term? For instance the prime number 2 geometric series.
What happens is that every number divisible by the number 2 disappears from the finitely factored rationals series and every number divisible by 2 disappears from the infinitely factored rationals series. Poof they are gone from both series. If we put the the the prime number 2 geometric series term back in the expression, boom, all numbers divisible by 2 re-appear in both series. The two sets (with finitely factored and infinitely factored elements) are bound together by the prime geometric series. One cannot exist without the other. Yes, connected, intertwined, bonded... Merged. Perfect balance. I realize I am mixing sets terminology here with series terminology. The generated finitely factored series implies the existence of the finitely factored set (the regular rationals), and the generated infinitely factored series implies the existence of the set of rationals where every element is infinitely factored and neither set can exist without the other.
And how is a prime geometric series in anyway related to the concept we call gravity and is a great expansion on that concept? One of the most famous properties of what we call gravity is the inverse square law. I can't think of a greater expansion on the idea of inverse square than the entire geometric series, instead of just a single element - inverse square.
So what is the 4th level, 4th density? The third density is the finitely factored set of rationals and its parallel infinitely factored set of rationals. This is the first level where we have a true field, the rationals, and the parallel infinitely factored rationals field. The finitely factored field if I understand properly is Archimedean and the infinitely factored field is non-Archimedean. There are also a couple of properties I think that popup from third density.
3rd Density property 1:
---------------------------
Each term of the infinite product expression (a prime geometric series) has a square range.
What do I mean? The 2 prime geometric series, for any exponent there is an inverse exponent. The distance between the two is square.
Example: The distance from 210 to 2-10 is 220.
In fact the distance between 2n and 2-n for any integer n, is 22n.
The range is square to every infinite n exponent. A perfectly square nature.
And if each term has a square range, then the range of the entire infinite product expression is:
22n x 32n x 52n x 72n x ... = (2 x 3 x 5 x 7 x ...)2n
The entire infinite product expression has a perfectly square nature.
The geometric object that I know of that is perfectly square, is a plane.
---------------------------
3rd Density property 2:
---------------------------
Each prime geometric series is a loop.
What do I mean?
Each prime geometric series has an infinity in two directions.
The positive integer exponent keeps growing larger and larger to infinity. There is no upper bounded integer exponent.
The negative integer exponent keeps growing smaller and smaller to infinity (approaching zero). There is no lower bounded integer exponent.
I propose this could be a loop similar in the way that in thermo-dynamics it is proposed that the highest temperature possible is anything below absolute zero, the highest and lowest temperatures possible wrap around in a loop.
---------------------------
If these properties are possible, then it is possible that the infinite product expression geometrically is a cylinder.
Forth level / density builds on third density by implementing Euclid's idea of introducing a real valued variable into the exponent (as in Eulcid's zeta function), but here we implement the real valued variable over the rationals and not just the inverse naturals as Euclid did.
This results in an infinite product that looks like:
Figure 4 (Infinite product expression for 4th density)
View attachment 108133
For each real value of s, there is a unique/distinct infinite product, which creates a unique/distinct finitely factored series and a parallel unique/distinct infinitely factored series. Which implies for each real value of s, there is a unique/distinct finitely factored Archimedean set and a parallel unique/distinct infinitely factored non-Archimedean set.
Fourth density is like a field of fields. Because there are uncountably infinite values for the real valued variable s, there are uncountably infinite pairs of Archimedean and non-Archimedean fields as in a continuum. You can look at each value of s as a slice that creates a unique/distinct Archimedean and non-Archimedean pair of fields.
The real valued variable s, also introduces the possibility of a much larger second loop like structure geometrically, as the reals also have property 2 and property 3 of third density and this may curve the cylinder of third density into a torus.
I believe the Archimedean fields have a space like metric and the parallel infinitely factored non-Archimedean field metric is ???
Fifth and Sixth level / densities
5th and 6th densities simply build on 4th density. 4th, 5th, and 6th have a similar profile. In fact 5th and 6th are achieved simply by using the same infinite product expression of 4th density and expanding the real valued variable s to include all of the infinitely factored numbers that are extant from all of the infinitely factored parallel sets. This would be like expanding the infinitely factored variable s to include something like the hyper-reals and the surreals.
In fourth density the finitely factored sets have numbers where every number has a finitely factored base and a finitely factored exponent. In fourth density the infinitely factored parallel sets have numbers where every number has an infinitely factored base and a finitely factored exponent.
When we expand the real valued variable s to all infinitely factored numbers, what were finitely factored numbers with finitely factored bases and finitely factored exponents of 4th density now have finitely factored bases with infinitely factored exponents, every number is now infinite. This is fifth density.
The parallel infinitely factored numbers of 4th density, where each number had an infinitely factored base and a finitely factored exponent now have infinitely factored bases and infinitely factored exponents. This is 6th density.
5th and 6th density are bound together also by gravity (the prime geometric series), neither can exist without the other.
That's it.
I equate the finitely factored sets as space like and the parallel infinitely factored sets to be??? not-space-like, maybe energy or consciousness or both. The first four levels/densities are one-half space-like and one-half not-space-like. Densities 4 through sixth have the same profile by the introduction of the variable in the exponent and the possible double loop of the cylinder.
I think these are the densities. I think this is what the secret scientific intelligence matrix has known about for some 60 to 80 years. The information in itself is not dangerous at all. But they have spent 60 to 80 years developing new mathematics around this new paradigm and it is the new mathematics and applying it to new physics and new weapons, etc. that is dangerous.
Here is a very simplistic diagram of the current paradigm:
Current Math/Science paradigm / world view (1)
View attachment 108136
All of mathematics, science and engineering comes out of this current paradigm. The cloud at the top contains thousands of more entries. I just put a few in.
The new paradigm (2) and new math should be built on this.
View attachment 108137
This all arises once we un-limit a couple of very limited definitions that tell us prime numbers can only create finitely factored numbers and we quit seeing only what we wish to see.
I know I don't always use the proper terminology. But I am pretty sure of what I see and I am trying my best to communicate that.
I think the missing link that the C's sessions said was earlier in the mathematical process is paradigm 2. What could be earlier in the process than the fundamental foundations of arithmetic? I think the fundamental foundations of arithmetic in paradigm (1) is true, but it is a half truth. I think the fundamental foundations of arithmetic in paradigm (2) is the objective reality.
I think Ark is in that cloud of paradigm (1). I am sure there are thousands of useful things that have arisen in paradigm (1) that apply to and are useful to paradigm (2), but paradigm (2) probably requires a whole lot of new mathematics also.
I think under paradigm (2), that dozens of the C's session answers about science and math begin to make sense. There are literally dozens of them.
Here are a couple of C's session quotes. Not the most astonishing that apply to paradigm (2), but interesting none the less.
=========================================
Session 22 July 2000
=========================================
The "trick" that 3rd density STS life forms will learn, either prior to transition to 4th density, or at the exact juncture, is to think in absolutely limitless terms.
=========================================
This C's excerpt is more like a prophecy, "think in absolutely limitless terms". Limitless terms (infinitely factored numbers).
=========================================
Session 13 June 1998
=========================================
A: You must remember mosaic, matrix... When you are on the verge of quantum changes or discovery, the realities begin to reveal their perfectly squared nature to you.
=========================================
Session 18 July 1998
=========================================
Q: (T) Fourth density. (A) We were told earlier that this UFT opens the door to other densities...
A: Yes.
Q: (A) And, some time ago Santilli was here and he had his own idea about UFT; gravity and anti-gravity, and he was told that he had a good idea of UFT, but that he only has one seventh of the equation. I don't understand why UFT has to go to other densities? Does it follow, or is it necessary once we have UFT, that the other densities will become clear in that they are necessary? How is it?
A: Fragmented inquiry.
Q: (A) Can we have a UFT which unifies EM and gravity and does not include the concept of other densities. In other words, can we put in a textbook all about the gravity and electromagnetics, and a student could learn all of this and still know nothing about other densities?
A: No. Other densities become apparent when...
=========================================
Session 10 July 1999
=========================================
Q: (A) Okay, no clue there. Now, next question relates to the story of creation which L wrote for the website, and I was reading it and trying to make sense, to make it not contradictory, and I found that it is not easy because many of the concepts that are used during these sessions are somehow contradictory to each other or they don't quite fit with the standard meanings of these concepts, so I wanted to ask for some explanation. First, we were told that gravity is essentially the most universal force and that it is from this that everything originates...
A: Gravity is the binder.
Q: (A) But, my question is: gravity is a term that is defined in dictionaries and encyclopedias and is a term which has a very precise meaning for physicists and mathematicians. I want to know if you are talking about the same thing or if you are using the term 'gravity' to describe something completely different that we know as gravity. Are we talking about the same thing?
A: Well, are you certain these "definitions" you speak of are not limited?
Q: (A) Yes, I am sure they are limited. Nevertheless, they are precisely defined concepts and you are using the same term 'gravity,' so I am asking if we are talking about the same thing, or if you are talking about something completely different?
A: How about a great expansion upon the same concept?
=========================================
Session 4 January 1997
=========================================
A: Please... we are drifting! Tell A that "aether" is Terran material science's attempt to address ether. The trouble is, there is simply no way to physicalize a plane of existence which is composed entirely of consciousness. It is the union of perfect balance between the two "states" or planes, that is the foundation and essence of all creation/reality. You cannot have one without the other!
Q: (L) When you say the two states or planes, you are saying the physical state and the state of consciousness...
A: Yes.
Q: (L) And you can't have one without the other. And the state of consciousness and the state of material existence are so completely connected, that both are infinite? One cannot exist without the other...
A: Yes, connected, intertwined, bonded... Merged.
=========================================
There are dozens more C's excerpts that apply.
And I want to mention just one quote from a forum thread about 'Krzysztof Jackowski - Polish Clairvoyant'. I know so much of the prophecy stuff is just nonsense, but sometimes they pickup on something. It seems as if the forum has a lot of activity regarding prophecy and AI threads recently.
'Krzysztof Jackowski - Polish Clairvoyant'.
=========================================
Schwab - Jan 20, 2023
=========================================
"Benetta"… I don't quite understand what I'm going to say, but he belongs to some "Benetta Club". The first sentence that came to mind. In criminal matters, too, I have a sense of things I don't understand, and I say them. The essence of the matter is to reach the missing person, the body, or the living person. You have to say or write down aloud what comes to mind.
There is an elite club. No more than 15 people belong to this association. Or maybe it's a group of 15 people. It's called "Benetta". I have absolutely no idea what that means.
[He Googles "Benetta", but couldn't find anything sensible]
He is an intermediary. He doesn't belong to this club. He is like an ideological intermediary, a connection. As if these 15 people did not want to reveal themselves or be politically active. We have this forum in Davos, he can go there, but no one from this club will go there. I do not claim that he is the only intermediary, there may be more of them...
Strange... Something is going wrong in his opinion and he fears that people may be awakening prematurely. "Logo Arithmetica". What is happening in the world right now, I'm not talking about Ukraine, but other things, it's also about people, this is the "Logo Arithmetica". Something is going wrong with it, and he's afraid of waking people up too soon.
=========================================
Thank you for your deeply insightful post. I'm drafting something I'm calling "The Architecture of Coherence," as the paper intended to be a kind of bridge of those areas - from abstract mathematics to a functional cosmological model. So this proposes similar foundational shift you're talking about, moving from a substance-based worldview to a resonant ontology where reality emerges from patterned coherence and information. Your concept of two parallel sets -finitely and infinitely factored, "connected, intertwined, bonded" is functionally described in the model as a "union of perfect balance between two 'states' or planes". This duality is seen in the complementary roles of the Ark (structural coherence) and the Grail (dynamic flow), or the inward recursion of Knowledge and the outward recursion of Life.
The number-theoretic "gravity as binder" may be the arithmetic description of the model's "geometry of coherence" - in the "Blueprint", where resonance principles and toroidal topologies define how the system is held together. This connects directly to your idea of "Logo Arithmetica," as the paper’s Unified Resonance Language Hypothesis posits that sacred language is not merely symbolic but is a functional, geometric code for modulating this field of reality.
This brings me to your crucial question about the "next step." - to move beyond pure math into application. The next stage involves empirical validation and practical use. Perhaps experimental pathways, including using cymatics to visualise the geometry of sacred phonemes and EEG to measure neurocoherence during their use. Perhaps even practical applications in fields like AGI, cognitive science, and linguistics - creating new therapies and technologies based on the principle of resonance and field modulation. Really the benefits is in it being testable framework as a cosmological model. It seems this is describing the same fundamental, coherent reality from complementary viewpoints.
Love to hear your thoughts / feedback.
Attachments
John G
The Living Force
I've seen Tony Smith's use of the Stan Tenen Meru Foundation 3x3x3 =3^3 = 27 element cube. He like you mentions it connects to the 10 element Sefirot (by ignoring order). Laura relates the densities to the Sefirot in an information theory kind of way. Tony also mentions your X,Y,Z = -1,0,1 as I,T,F where I is indeterminate and he expands the I to TF and FT which gives a more spacetime 4x4x4x4 = 4^4 = 2^8 = 256 = the elements of the Cl(8) Clifford algebra. I noticed you also mention Clifford aka geometric algebra. You can also relate to Jungian and Enneagram personality models with this structure as well as cellular automata and lots of sacred geometry (in addition to the Sefirot and Enneagram) so it would as you say be a versatile structure. Ark is currently playing with the 2^3 = 8 element heart of the structure. It's the biquaternions and like with I to TF, it was interesting to see multivectors that can be used as spacetime basis vectors though that would be more like I to TF and 0 since order is ignored.Thank you for your deeply insightful post. I'm drafting something I'm calling "The Architecture of Coherence," as the paper intended to be a kind of bridge of those areas - from abstract mathematics to a functional cosmological model. So this proposes similar foundational shift you're talking about, moving from a substance-based worldview to a resonant ontology where reality emerges from patterned coherence and information. Your concept of two parallel sets -finitely and infinitely factored, "connected, intertwined, bonded" is functionally described in the model as a "union of perfect balance between two 'states' or planes". This duality is seen in the complementary roles of the Ark (structural coherence) and the Grail (dynamic flow), or the inward recursion of Knowledge and the outward recursion of Life.
The number-theoretic "gravity as binder" may be the arithmetic description of the model's "geometry of coherence" - in the "Blueprint", where resonance principles and toroidal topologies define how the system is held together. This connects directly to your idea of "Logo Arithmetica," as the paper’s Unified Resonance Language Hypothesis posits that sacred language is not merely symbolic but is a functional, geometric code for modulating this field of reality.
This brings me to your crucial question about the "next step." - to move beyond pure math into application. The next stage involves empirical validation and practical use. Perhaps experimental pathways, including using cymatics to visualise the geometry of sacred phonemes and EEG to measure neurocoherence during their use. Perhaps even practical applications in fields like AGI, cognitive science, and linguistics - creating new therapies and technologies based on the principle of resonance and field modulation. Really the benefits is in it being testable framework as a cosmological model. It seems this is describing the same fundamental, coherent reality from complementary viewpoints.
Love to hear your thoughts / feedback.
Trending content
-
Thread 'Coronavirus Pandemic: Apocalypse Now! Or exaggerated scare story?'
- wanderingthomas
Replies: 30K -
-
-