G
Guest 15258
Guest
If we identify all points A in R4 with A + u for some fixed point u in R4, then we get a space which is homeomorphic (for all intents and purposes exactly the same) to R3 x S1. This is a product space, and is exactly like R3 with an additional Kaluza-Klein dimension. What I don't like about this space is that there seems to be a preferred direction.
If we suppose that the term "density" refers to ether density, and that the perceived structure of space comes about as a result of the interactions of ether particles (i.e. space looks the way it does because of the way light travels through it,) and if the set of ether particles is discrete then I think maybe the Kaluza-Klein stuff makes more sense. But I think this then means that space is discrete, which maybe has more problems.
A few years ago there was a discussion on the Electric Universe forum where they were talking about space as being a fluid. They said that if you look closely enough at a fluid it no longer looks continuous. I gathered that the idea was that quantum effects start to appear when you look at scales where space no longer appears continuous. This fits with in with the idea of discrete space.
Anyway here's another picture,
If we have a pantagon in R4 arranged in a specific way, then under a specific map from R4 to R3 x S1, one of the points gets mapped to some point on the opposite edge. I don't know if what Lethbridge found was that pentagons in 3D are just one triangle in 4D or if they are two.
If we suppose that the term "density" refers to ether density, and that the perceived structure of space comes about as a result of the interactions of ether particles (i.e. space looks the way it does because of the way light travels through it,) and if the set of ether particles is discrete then I think maybe the Kaluza-Klein stuff makes more sense. But I think this then means that space is discrete, which maybe has more problems.
A few years ago there was a discussion on the Electric Universe forum where they were talking about space as being a fluid. They said that if you look closely enough at a fluid it no longer looks continuous. I gathered that the idea was that quantum effects start to appear when you look at scales where space no longer appears continuous. This fits with in with the idea of discrete space.
Anyway here's another picture,
If we have a pantagon in R4 arranged in a specific way, then under a specific map from R4 to R3 x S1, one of the points gets mapped to some point on the opposite edge. I don't know if what Lethbridge found was that pentagons in 3D are just one triangle in 4D or if they are two.
John G
The Living Force
One problem I think is that our spacetime is actually already a three space, one time metric while the Cs talk about a 4th non-Kaluza Klein space. For a Lethbridge interpretation, it actually makes more sense to have the visualized pentagrams be a visualization for 4th density and have the appeared triangles of fire be an observation in 3rd density. You would effectively be turning a 4-dim all space metric into a 3,1 metric where the S1 is time for third density. I also wonder if your map turning a pentagon into two triangles via mapping a vertex to an edge point could also map a 5-vertex 4-dim 5-cell to the 4-vertex 3-dim tetrahedron via mapping a vertex to a cell point thus relating to the clue about what a tetrahedron in 3D is in 4D. R4 is also homeomorphic to R3xR1 right off the bat so going spherical for your map with S1 (cylinder) before S3 (torus) is kind of just turning R1 to S1. There's no problems with a discrete spacetime. Models like Loop Quantum Gravity and Feynman Checkerboards do that already.
Last edited:
John G
The Living Force
A couple of people here hinted that it would be nice if this was simpler. I once said to Tony that I wished triality (a math concept used for physics) was easier to understand and he replied that he wished it was easier to understand also. This is kind of an area where the more time you put into understanding it, the harder things get to understand (you previously would just conveniently skip over those hard parts). I'm going to use Tony to make this as simple as I can. At the level I understand it, it actually isn't as difficult as it often sounds.
For this link Tony got mentioned for the 24-cell which is a 4-dim shape. One simple way to picture a 24-cell is to start with how you can picture the 3-dim cuboctahedron using 2-dim shapes. The cuboctahedron is simply starting with a 2-dim hexagon and adding above it and below it, 3-dim equilateral triangles. This gives you 6+3+3=12 vertices in 3D. Now start with the 3D cuboctahedron and add above and below it in the 4th dimension, the 3D six vertex octahedron (diamond shaped thing). This gives you 12+6+6=24 vertices in 4D (the 24-cell).
The cuboctahedron inside the 24-cell represents Ark's conformal gravity. It's the hexagon the Cs talk about. The actual hexagon would connect a vertex on 6 different axes: XYZTzt. The cuboctahedron representation though is 3D so it sticks the 6 dimensions as endpoints of 3D axes (XY ZT zt). A point like XT would be a vertex of the cuboctahedron (negative one on the XY axis, positive one on the ZT axis). The zt axis would be curled up Kaluza-Klein dimensions added to the normal XYZT ones. The other not mentioned yet axis (xy) would add in the two octahedrons to get the 24-cell and for Tony relates to positive and negative charges of the non-gravity forces.
Now let's switch away from geometry to information bits since information is fundamental. We have 8 bits (XYZTxyzt) where say the XT boost of Ark's conformal gravity would have the X and T bits as ones and the rest as zeros. XY would represent a rotation in the XY plane. XZ and YZ would be rotations for the other two planes. XT, YT, and ZT (boosts) as one bits would be for constant velocity movements. Xz, Yz, Zz, Tz (translations) get related to the cosmological constant that expands the universe. Xt, Yt, Zt, Tt as one-bits are special conformal transformations that can relate to complex number shortcuts through spacetime (thus making our 8-bit information an octagonal complexigram).
So far we've only looked at force particles (two one bits). No one bits at all is the Higgs scalar (used for the matter mass generating Higgs mechanism). A single one bit (X Y Z T x y z t) are the spin spacetime components of the neutrino. Three one bits like Xxy would be the X spin component of a red down quark. The cases where the three bits are all capitals or little letters (YZT, XZT, XYT, XYZ, yzt, xzt, xyt, xyz) would be spin spacetime components for the electron. Four one-bits are for 4-vector spacetime fields which have much of the same structure as two one-bit force particles since they are force fields. This lets you do things like curve spacetime and accelerate your matter (and antimatter). It does have some additional structure not seen with the force particles related to Ark's questions to the Cs about bimetric gravity.
The five one bits can be treated like three zero bits and related to antimatter (antiquarks and positrons) spacetime components in the same way as the three one bit quarks and electron. The 7 one-bits (1 zero bit) for the antineutrino spacetime components can be treated like the 1 one-bit neutrino components instead using the 1 zero bit. The 6 one-bits can be treated like 2 zero bits and are used as the ghosts of the two one bit force particles (Fadeev Popov ghosts are needed for Feynman path quantization). The all ones is the ghost of the all zeros Higgs scalar.
Stella Marys
Jedi Master
Thank you Archaea for the link you provided: platonic. Seeing the figures helped to better materialize the words that you want to represent those figures. It really is a visualization exercise to look closely at those geometric figures. It's like making a new "space" in your mind.
It requires a new way of making movements in the mind. I remember the year 2013, when I entered art school (one year only), I chose sculpture. At first it was difficult for me to express the three dimensions of space (nowadays, it is still difficult to understand 3D, it is a work in progress) in sculpture you work with volume in space. It was the first time that I was aware of the 3D. I realized that in formal education, we are not taught to visualize these 3D correctly.
In secondary school you don't go into geometry in depth. Just a little technical drawing, with the beloved projections, but it's flat geometry practically. I think this thread is fundamental to "stretch" the mind. I follow the thread closely, I learn with you.
I'm fascinated by this figure:
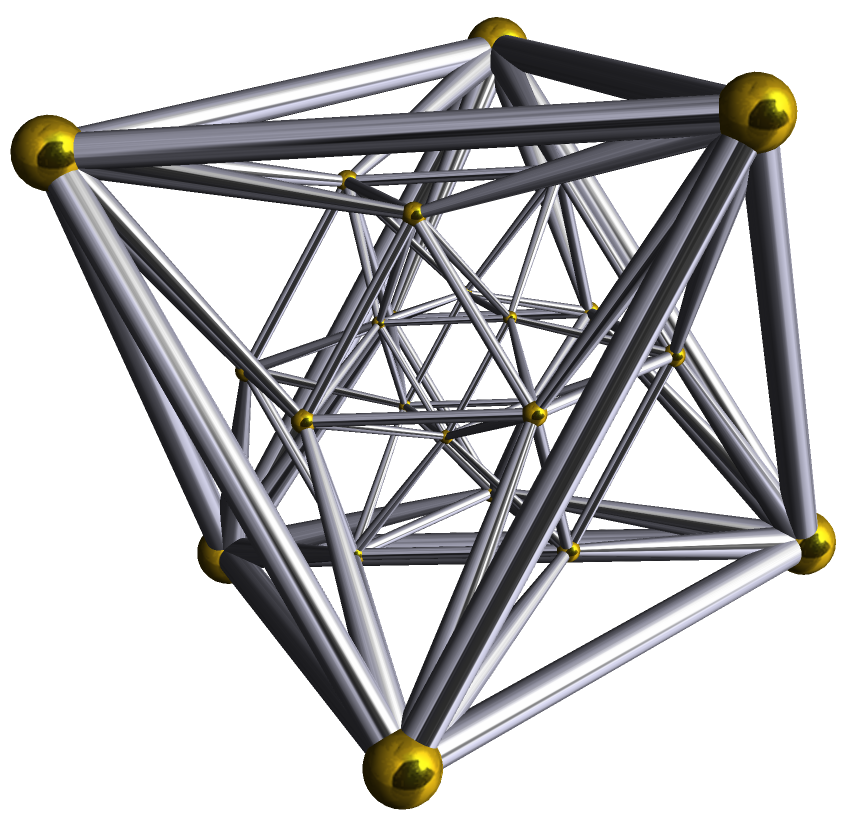
en.wikipedia.org
It requires a new way of making movements in the mind. I remember the year 2013, when I entered art school (one year only), I chose sculpture. At first it was difficult for me to express the three dimensions of space (nowadays, it is still difficult to understand 3D, it is a work in progress) in sculpture you work with volume in space. It was the first time that I was aware of the 3D. I realized that in formal education, we are not taught to visualize these 3D correctly.
In secondary school you don't go into geometry in depth. Just a little technical drawing, with the beloved projections, but it's flat geometry practically. I think this thread is fundamental to "stretch" the mind. I follow the thread closely, I learn with you.
I'm fascinated by this figure:
24-cell - Wikipedia
Looking at the images you put here, the vertices and axes, tell me, do you think there is a relationship between the geometry we see here and how we interpret the geometry of the atomic arrangements in the elements and other chemical arrangements? Maybe we can't fully understand 4th density geometry if we don't observe that 4th density is half ethereal and half physical. In that sense the changes in the geometry of an element or chemical link changes the properties of the same making it either more physical or more ethereal.
This thread is way above my head, but I had a thought about art today. When you draw, you're representing a 3D object on a 2D surface. But you can also sculpt, which is making a 3D object in 3D.
Then you can use a computer program to model a 3D object. But that is still 2D, because it's on a screen and you can only see it from one angle. But if you animate it, you're sort of virtualizing the third dimension across time within the program.
So what about 4D? Do they make works of art that have 4 dimensions that are represented in 3 dimensions? Can you take a 3D program and model a 4D object? You'd need another dimension, right? I guess it has to be your mind that adds the extra one? I'm thinking about the book Consciousness: Anatomy of the Soul.
If you could take all of the time slices of a hypercube animation and put them together and somehow extract them into "hyperspace" or the 4th dimension, would you see it in your mind's eye as a real hypercube?
Then you can use a computer program to model a 3D object. But that is still 2D, because it's on a screen and you can only see it from one angle. But if you animate it, you're sort of virtualizing the third dimension across time within the program.
So what about 4D? Do they make works of art that have 4 dimensions that are represented in 3 dimensions? Can you take a 3D program and model a 4D object? You'd need another dimension, right? I guess it has to be your mind that adds the extra one? I'm thinking about the book Consciousness: Anatomy of the Soul.
If you could take all of the time slices of a hypercube animation and put them together and somehow extract them into "hyperspace" or the 4th dimension, would you see it in your mind's eye as a real hypercube?
G
Guest 15258
Guest
Did the C's say that 4th density was like a Kaluza-Klein dimension or that it wasn't? I remember them saying that there is no difference, but I can't find it now.
Is there somewhere where I can read about what Lethbridge actually wrote, I was going by this,
So I had a pentagon in R4 map to triangles in R3 x S1, which is exactly like a Kaluza-Klein dimension. The idea is that with a discrete number of ether particles, there's more than one map from R4 to R3 x S1.
Yeah, but I like continuity.
What's triality?
This is an interesting direction, it's completely different to what I'm thinking.
No worries, I'm glad you like this thread.
I sometimes think that being able to visualize only 3 dimensions is very limiting. After thinking about the different densities and how they might relate to platonic solids I came to the conclusion that maybe it's possible for some consciousnesses out there to comprehend, visualize and experience n dimensional space for any n.
Because of this I had a go at meditating on and attempting to visualize 4-dim space. I think maybe it's possible, but I haven't managed to do it yet.
I think there's a relationship, but with chemical elements the geometry is contained to 3 dimensions only. Whereas I think for the ether there are infinitely many dimensions. Or the space itself emerges from the "geometric" relationships.
That's what I think too.
We could experiment with looking at tesseracts and the other 4 dimensional platonic solids using VR. Then we can see these 4 dimensional objects projected into 3D instead of just 2D.
John G
The Living Force
They said it's an added spatial reference to visualize inward and outward at the same time not a Kaluza-Klein dimension.
From the 11/14/98 session:
I think they mean an S3xS1 spheritorus where one can sort of sit on top of an S3 sphere and see around via the S1 to the inside of that same sphere.
Session 5 August 2017
etezete et Mandrak : Merci pour vos explications et diriger l’énergie... Etezete and Mandrak: Thank you for your explanations and direct energy ...
cassiopaea.org
You can project a 4-vertex 3D tetrahedron into its 3-vertex 2D triangle base. Similarly you can project a 5-vertex 4D 5-cell into its 4-vertex 3D tetrahedron base. Course maybe it has more to do with the 5-pointed star pentagram being a pentagon inwardly and triangles outwardly as in what the extra 4th dimension lets you view at the same time?
John G
The Living Force
It's a math property that lets the spacetime (vector) and number of spin components for matter and antimatter (spinor) to be equal in 8 dimensions.
Physics application of $SO(8)$ and Spin(8) triality | PhysicsOverflow
Triality is a relationship among three vector spaces. It describes those special features of the Dynkin ... :54 (UTC), posted by SE-user wonderich
Tony is like Ark up through conformal gravity but Tony just cited someone else for the bimetric 4-vector part so it's more like they are both bimetric gravity researchers in a more general sense. They also both in general seem like ER=EPR-like objective collapse researchers. I don't think either is upsetting the standard model too much; they are mostly unconventional for gravity.
We see in this way as above.Below is "prism" image from wingmakers.
This is 'mirror' density for me. Same object have many layers. If you do 3d graph in plane for platonic is same abstract representation of 3d in 2 d. But how you can represent one object in multiple layers from 4d in 2d??? You can draw multiple object as layers as you would represend 3D in 2d drawing You see it as one object in many layers, but none layer is 100% solid.
It is when you take a crystal and see layers around this objects throught this crystal.
[QUOTE = "Pearce, message: 882028, membre: 11297"]
J'espère bien qu'en 4D nous aurons rapidement une sorte d'introduction à la nouvelle classe de géométrie - mon pauvre cerveau primitif ne peut tout simplement pas la saisir maintenant
[/CITATION]
Idem pour moi, je suis toujours émerveillée par vos explications qui me font rêver mais qui me laissent toujours en arrière ... Merci quand même de partager toutes vos réflexions ...
Same for me, I am always amazed by your explanations which make me dream but always leave me behind... Thank you anyway for sharing all your thoughts...
J'espère bien qu'en 4D nous aurons rapidement une sorte d'introduction à la nouvelle classe de géométrie - mon pauvre cerveau primitif ne peut tout simplement pas la saisir maintenant
[/CITATION]
Idem pour moi, je suis toujours émerveillée par vos explications qui me font rêver mais qui me laissent toujours en arrière ... Merci quand même de partager toutes vos réflexions ...
Same for me, I am always amazed by your explanations which make me dream but always leave me behind... Thank you anyway for sharing all your thoughts...
How you can vector light?
In 3d plane light seems solid (this is like paper for 3D drawing). So in 4D perception light is layered. It means is more or less dense in perception.
More density is less time. More time is less density and gravity binds it?
If 2000 years(more time, life span) is in space(less gravity condition) then 800 years is less time and more gravity on earth condition.
Space is constant.
In 3d plane light seems solid (this is like paper for 3D drawing). So in 4D perception light is layered. It means is more or less dense in perception.
More density is less time. More time is less density and gravity binds it?
If 2000 years(more time, life span) is in space(less gravity condition) then 800 years is less time and more gravity on earth condition.
Space is constant.
