19 Year Cycle Lunar Standstill Upcoming

[Guest]

Hi Lynne, Anders, Vulcan, and Everyone...

I'm glad to hear you're all still here and doing fine, and no one is reporting any strange and creepy "window fallers":D
...but actually it's Sue who's doing the headcount.

My apologies, Sue. I guess I got confused by the way the names "Sue" and "Lucy" look so much alike. (Yeah, right.)

That's alright Lynne, it happens all the time. :)

 

[Ryan]

I drove to the NSW countryside and enjoyed the excellent hospitality of friends/fellow Aussie QFG members for the occasion.

It was a fairly low-key event; we just sat quietly and tried to connect with other group members around the world while contemplating the suffering of the Lebanese and Iraqi people, and tried to hold a shared intent for a more creative future. I didn't really notice any "effects" or "phenomena", although I did feel a little pressure and warmth in my solar plexus area.

Much more spectacular in the "phenomena" area occurred the previous night when we were out walking and saw a very clear and impressive fireball burn up in the sky. It was easily the biggest meteor/fireball I've ever seen, covering about 30-40 degrees of sky on its descent, with a visible smoke trail and faint, high-pitched whistling sound.

It made the hairs on the back of my neck stand up, I'll say that! Perhaps a symbol of some kind?

 

[Renaissance]

The weather here in Rhode Island was more unique than most other days. Clouds covered the sky, there was a cool breeze - sometimes turning into strong winds. Rain was called for the whole day but something in the air seemed to hold it back. I dressed in as much silk as I had and did some walking early in the day. After walking a bit I rested and felt the heat generated from the multisilk layers. After sometime I felt an intense heat in my chest which rose to my head, which felt to be a different sensation of normal physical body heat. I also had a lack of appetite during the whole day.

After my walk I returned home and decided to try and dream a little. In one of my dreams I remember being in some remote area of a forest trying to contact Joe with my mind. There were other people with me in the dream but I don't remember all of who they were.

I woke up about a half hour before the event and decided to go outside. the weather was amazing - the wind was blowing, the overcast sky seemed full of life. I did some spins and felt like dancing during the spin. Bad idea - I lost control for a bit and nearly toppled over. Afterward I spread out on the grass and looked up at the sky thinking about the group and our world.

 

[Tenten]

In the kitchen of the appartment, in the dark, with a small candle, I offered my empathy to the world, without expectation. Kneeling on the floor, I thought of all the sufferings all over the world and ask for help.

I continue the reading of "C of Z". In the same time, I am reading an other book from Grégoire Dumitresco "L'holocauste des âmes", the "Souls holocaust". It's the real life story of G.D when he was jailed by the Securitate in Pitesti, Romania in 149-1951. He described the"experiences" he lived through under the communist regime where they searched to create a new man, in fact a new robot. He made a accurate psychological description of the process of de-humanization and asserts the will the had to make men regress and behave like "robot". It's terrifying. A "ponerology" study.

 

[D Rusak]

Eek, I thought the thread died and didn't check.
Just to throw my account in, I came up with a plan (posted earlier) and pretty much followed it. I didn't get to go to the library because my roof sprung a leak again (3 times in one week) and my oven didn't work. Things went pretty smoothly with that, though. I read CoZ- maybe the first 1/4 or so, and also the cass article on the dervishes. I found a quote from that which seemed to correlate with existence according to the C's:

I died from a mineral, and plant became;
Died from the plant and took a sentient frame;
Died from the beast, and donned a human dress;
When by my dying did I e'er grow less;
Another time from manhood I must die
To soar with angel-pinions through the sky.
Midst Angels also I must lose my place,
Since 'Everything shall perish save His Face.'
Let me be Naught!
The harp-strings tell me plain
That unto Him do we return again and again.

I meditated on that and burned a paper with that inscribed immediately before spinning, and also prayed for Palestine/Middle East et al. It was interesting, I have not really "prayed" in a long time. Funny how praying sounds like preying. I didn't "pray" anything like I did when I believed in the "church" and all that, more of a meditation and concentration of will. A couple of months ago I experimented with spinning during breaks of practicing in an office chair (like when we were kids!) and found that even though I naturally want to spin to the right (clockwise) I would feel particularily clear for a lack of a better description when I spun to the left (ccw). Afterwards I had dinner and felt pretty good. I became restless and went for a walk, and discovered that several blocks nearby had their power knocked out for a while (sort of random in a major city).
I have noticed since then that I've been quite hungry. Also it has been much harder for me to study until later in the evening for some reason- luckily my schedule admits this somewhat. I've also been able to discuss topics with others that normally were not so cool about it, and people have been pretty receptive.

 

[EmeraldHope]

Back when Secret History was going through its first edits, Frank J (QFG
researcher) was quite fascinated by the discussion of the 19 year cycle.
He decided to do some research.

The graphs and things he included in his paper aren't included in the following, but they aren't necessary. What is important are his remarks as well as the upcoming event.

Those who have read "The Secret History of the World" are aware of the possible significance of this event.


19-year Lunar Cycles
By Frank J

I was inspired to put together this little paper by the discussion in
'Secret History' concerning the importance of the 19-year lunar cycle in the
cultures of some ancient civilizations, in particular the culture that
flourished around Stonehenge. The C's suggests that the 19-year cycle is a
window, gravitationally induced, for direct access by humans ("right
people, right place, right activity, right time") can directly access
higher dimensions without any help from other entities. by engaging in

group activities,
carried out in a geometric pattern, and
with certain amplification materials in particular geographic locations,
and
the participants having fused their magnetic centers,

And, of course, I am also interested in where we are now in that cycle.
The following explanations are cobbled together
from several scientific and archaeological sites on the Internet, and their
web addresses are provided at the end of this article.

Predictable motions of the earth's rotation axis on time scales less than
300 years are all referred to as nutation, a correction to the precession
cycle (26,000 years). The currently standard nutation theory is composed of
106 non-harmonically-related sine and cosine components, mainly due to
second-order torque effects from the sun and moon, plus 85 planetary
correction terms. The four dominant periods of nutation are 18.6 years
(precession period of the lunar orbit), 182.6 days (half a year), 13.7 days
(half a month), and 9.3 years (rotation period of the moon's perigee).

The primary nutation of 18.6 years drives two other observational cycles:
the Saros cycle (18 years and 11 days) and the Metonic Cycle (19 years)

Primary Nutation Cycle

The cause of this cycle is the precession of the lunar orbit about he Earth.
In addition, the Sun's gravitational pull leads to a precession of the
Moon's orbital axis, with a period of 18.6 years. This precession advances
the locations where the moon's orbit crosses the ecliptic (the nodes).
Eclipses will occur on the new or full moon nearest the time that the sun
passes one of the nodes

There are several observational consequences of this cycle, none of which
require a technical knowledge of the lunar precession.

Solar Eclipse Prediction

This cycle causes every eclipse of the sun to repeat itself at a different
place on the earth every 18.6 years. The effect of this "wobble" is that
eclipses seasons occur 365.24/18.6= 19.6 day earlier every year. Thus in
1997, the eclipse season of the fall will be centered about the node 19.6
days earlier than that of the previous year.

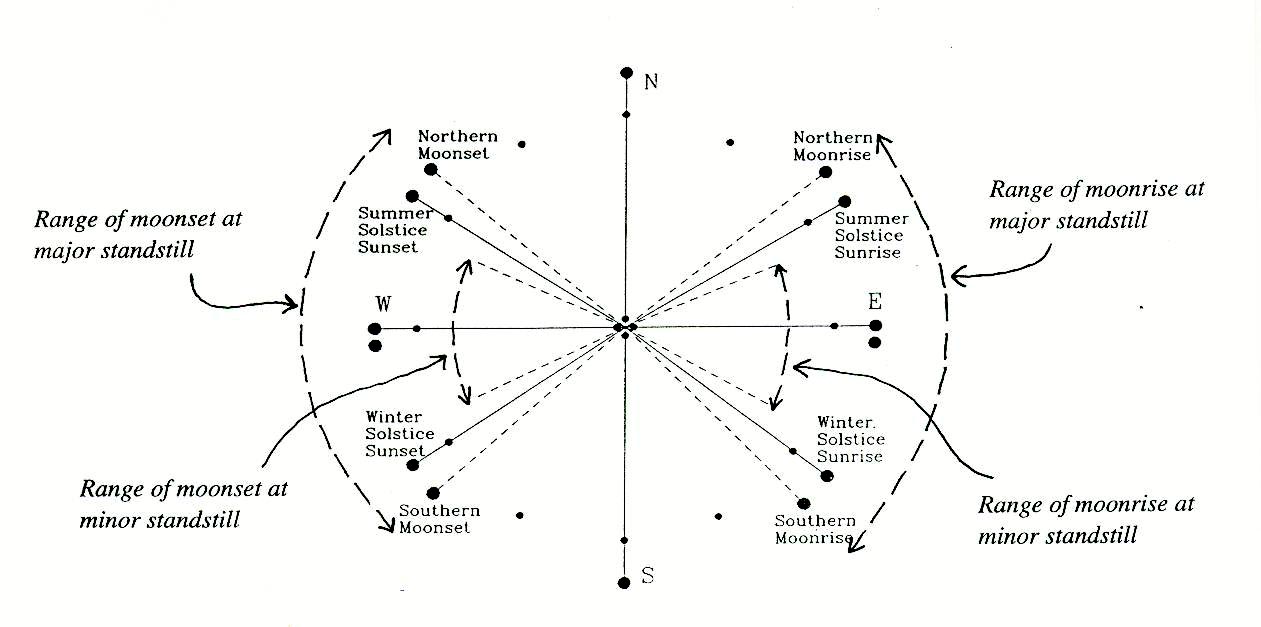
Lunar Standstills: Because of the 5.1 degree tilt of the moon's orbit with
respect to the ecliptic, the moon may be anywhere within 5.1 degrees above
or below the ecliptic. During major standstills the moon reaches a
declination of 23.5 plus 5.1 degrees or 28.6 degrees; major standstills
occur every 18.6 years. At minor standstill the greatest declination that
the moon reaches is 23.5 minus 5.1 degrees or 18.4 degrees.

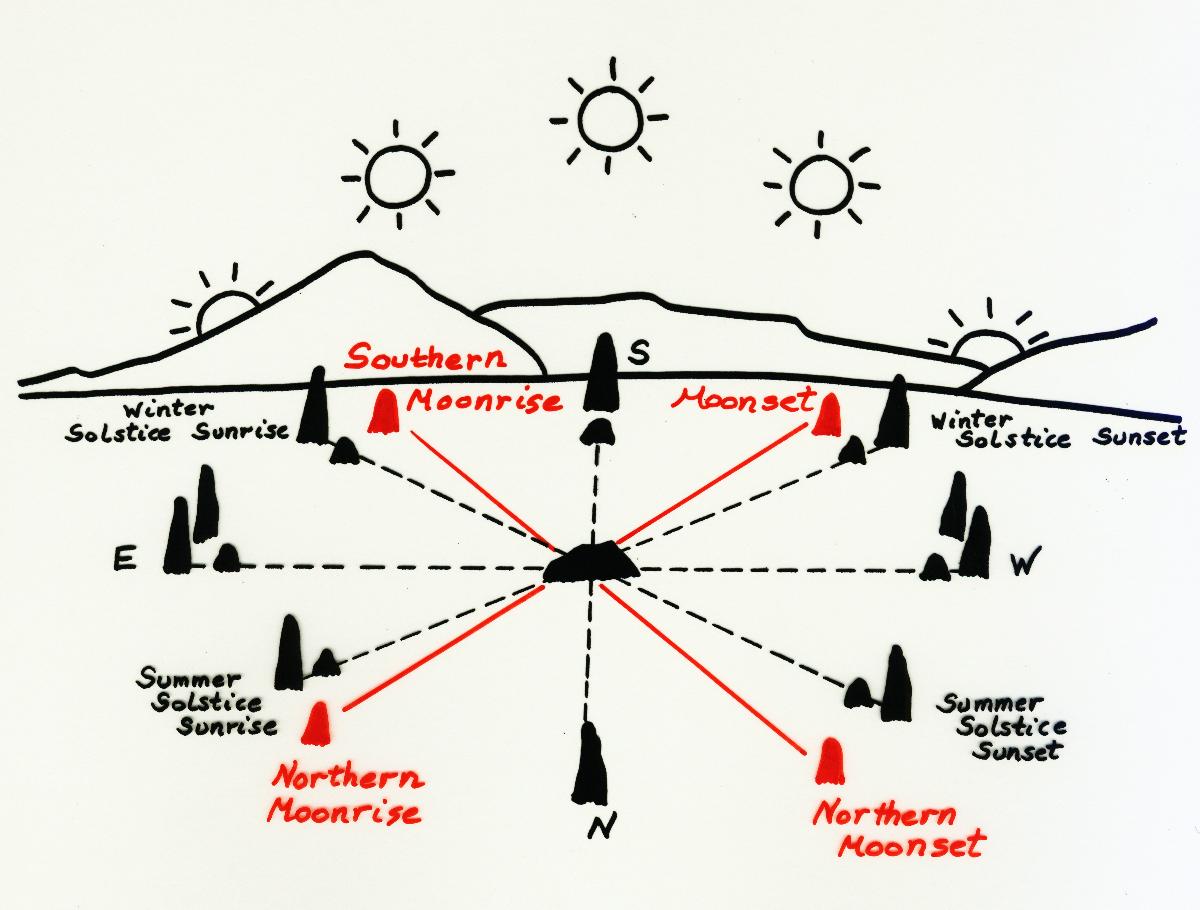
This means that every 18.6 years, the rising or setting Moon reaches a
northern extreme in rising and setting azimuth at summer solstice, and a
southern extreme at winter solstice. These are called major standstills.
While such standstills can in principle be determined using horizon
observations, as with the summer solstice Sun the Moon's year-to-year
angular displacement along the horizon at summer solstice is very small near
standstill. It should be noted that 18.6 years is measured from the point of
view of the lunar orbit. Observationally, from the Earth's surface, the
length of time between two major standstills is not 18.6 years: it switches
back and forth between 18.5 years and 19 years, and 18.6 years is an
observational average. This may become clearer by looking closely at the
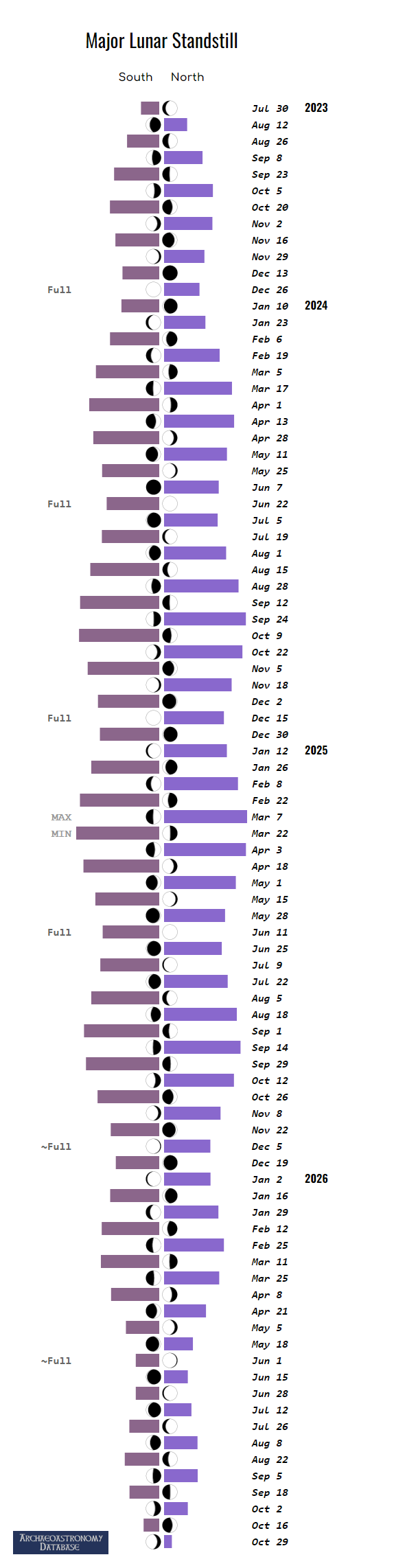
behavior of the moon at the time of her extreme positions. This chart shows,
for the current and three most recent nodal cycles, the maximum southern
azimuth position of the rising moon reached during each month for
approximately three years. The data shown are the maximum rising moons for
the periods Mar 1, 1949 - Mar 31, 1952; Sep 1, 1967 - Sep 30, 1970; Mar 1,
1986 - Mar 31, 1989; Sep 1, 2004 - Sep 30, 2007.


To understand what 'standstill" means observationally, it will be easier to
use the Sun as an example. The sun rises furthest to the north at the summer
solistice, around June 21 each year. Following the summer solistice it will
begin to rise a little further south each day, rising due east at the fall
equinox around September 21, and reaching its southernmost rising point at
the winter solistice around December 21. After the winter solstice the sun
will begin rising further north each day, rising due east at the spring
equinox around March 21, and finally reaching its northernmost rising point
again around June 21. The slow sweep of the sun's rising azimuth across the
eastern horizon takes a full year, and practically repeats itself exactly
from year to year. The rising point changes very little from day to day when
it's rising near either the northern or southern extremes of its motion.

This phenomenon is known as the "standstill." For several days around either
solstice the sun's rising azimuth will hardly change at all. In contrast,
when the rising point is between the extremes, say around the equinoxes, the
rising azimuth changes quite a bit from day to day. This phenomenon of
"standstills" near the extremes applies to periodic motion of many kinds,
including the motions of the moon.

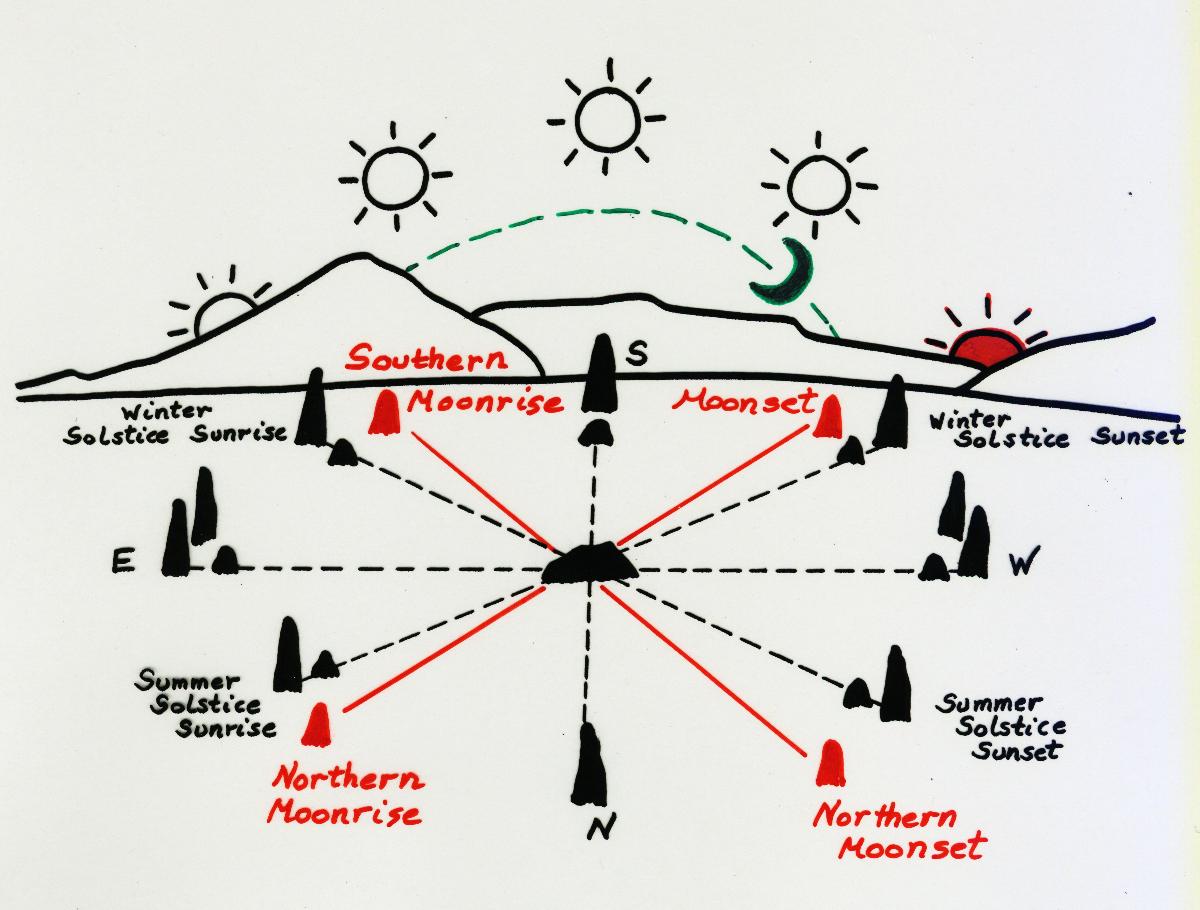
The rising point of the moon changes from day to day in a very analogous
way, marking out a sweep from north to south and back again, except that it
takes only one month to accomplish one complete cycle. The actual period of
this cycle is the "draconitic month" of 27.21222 days, on the average.

Unlike the sun, however, the extremes of the northernmost and southernmost
rising azimuths will not remain the same for each cycle. After noting the
northernmost rising point for the moon during one month, one may very well
find it rises at a point even further north the next month. In fact, there
is an 18.61-year variation in the extremes of the moon's rising point.


A major standstill limit will happen at the moment the moon is near a
quarter moon and the lunar node is near the vernal (or autumnal) point. The
moon is at his highest point in its orbit and combining this with lunar
phase, the sun is near equinox.


Saros Cycle

The periodicity of solar eclipses depends upon two lunar orbital cycles
coinciding with the moon passing through a node. First, a new moon occurs on
average every 29.530588 days. The moon's average orbital period, perigee to
perigee, is 27.554548 days. These cycles repeat every 18 years, 11 1/3 days;
or 6585.3211 days; or 233 new moons, approximately 239 perigees and 242
nodes. Every eclipse in a Saros family shares the same 18 year, 11.33 day
cycle.

Calculation:

223 lunar synodic months = 29.053059*223 = 6585.3216

242 lunar draconitic months = 27.21222*242 = 6585.3572


The Metonic Cycle

Another pattern evident in the table is that the solar calendar dates of
maximum moonrises often repeat, 19 years apart:
1 solar year = 365.2425 days

1 lunar synodic month (full moon to full moon) = 29.53059 days
19 years = 365.2425*19 = 6939.6075 days

235 lunar synodic months = 29.53059*235 = 6939.6887 days
This is a difference of only 0.0812 days, or about two hours. So, after
exactly nineteen solar years the sun will return to the same position
relative to the stars (by definition), and the moon will have very nearly
the same phase (just two hours difference). This fact was much appreciated
by the Greeks, as the dates of the new moon, full moon, etc., would repeat
every nineteen years.

For the purposes of maximum moonrises, the above coincidence alone would not
be enough to ensure that maximum moonrises will occur on the same date 19
years apart, it only guarantees the phase will be the same on the same
dates.

Another well-known aspect of the Metonic cycle is that since the sun, moon
and earth return to the same relative positions, the pattern of eclipses of
the moon and sun may repeat somewhat after 19 years elapses. The half-day
difference of the lunar draconitic cycle however is enough to throw the
eclipse repeatability out of kilter fairly rapidly, but three or four
eclipses may repeat, on the same dates 19 years apart, before this happens.

In any given year the solar calendar dates of Full Moon events will be
duplicated every 19 years. This creates a clear cycle connection that was
delineated by the mythic 19 Priestesses of Bridget. Each of these individual
"Priestesses" represented the "character" and experience of each of the 19
components of the Great Lunar Year. This relationship creates an excellent
basis for cyclic pattern divinations. A 19 year cycle upon which one can
hang other, shorter cycling patterns for delineation and understanding

Conclusion

So, I conjecture that the gravitational "window" in TIME that allows "the
right person, in the right group, at the right time and at the right place"
to access hyperdimensions is the standstill point, also called lunarstice.

When is the next one?

September 2, 2006

Ya'll bear with me here, as I do not know if what I am about to say has any meaning at all. I have been spending a lot of time on the Gog Magog thread, the Maze of Malta thread, and Apollo etc as related to the bear goddess.


Here we have a reference to Apollo dancing, and a reference to solar eclipse. As I mentioned in the Sol Niger - Black Sun thread, a solar eclipse is also an esoteric symbol for the black sun. But what just struck me, in relation to the goddess and perhaps which face one sees. is that the symbol for the Vesica Pisces could be either the beginning or ending of a solar eclipse, when the two or starting or ending overlap.


Also, that symbology could also represent the hynopompic or hypnogogic state ( There is Gog again, lol) One happens while going further to sleep, the other as one is closer to being awake. So here we have a "window". I do hope this does not come across as noise, as I do not mean for it to,. I always struggle whether to post obeservations like this or not, as they may not mean a thing.

 

[Jebra]

I'm bumping this old (and fascinating thread) as it's due in 2025. There are some real gems hidden in this forum aren't there? Maybe this time around there will be an added potency to it?

 

[ryu]

I'm bumping this old (and fascinating thread) as it's due in 2025. There are some real gems hidden in this forum aren't there? Maybe this time around there will be an added potency to it?

I saw your post and then read the thread, it's a gem indeed! 19 years have passed, it feels life back then was a century ago, without covid, mass surveillance...
Anyway, I'm all for a trying doing something in group next year! The Wave is here, the world is changing fast, we've learned a lot these last years and our collinearity as a group as gotten better. Maybe it could help.

 

[Gaby]

Well, I'm still not sure how he (Frank J) calculated the September 2nd, 2006. But we can study the cycle and with some networking, we can calculate the special day in 2024/2025. First, some basics:

Major Lunar Standstill -- Moon Teachings for the Masses

Sunwheel - Proposed and constructed under the watchful eye of Professor Judith Young of the Astronomy Department at the University of Massachusetts in Amherst

www.umass.edu

With the culmination of the 18.6-year cycle of the Moon in 2006 and again in 2024-25, also called the Major Lunar Standstill, we are afforded the unique opportunity to observe the monthly, annual, and 18.6-year wanderings of the Moon. The 18.6-year cycle is caused by the precession of the plane of the lunar orbit, while this orbit maintains a 5° tilt relative to the ecliptic. At the peak of this cycle, the Moon's declination swings from -28.8° to +28.8° each month. What this means is that each month for the years 2005-2007 and also 2023-2026, the Moon can be seen rising and setting more northerly and also more southerly than the solar extremes, and will transit monthly with altitudes which are higher in the sky than the summer Sun and lower in the sky than the winter Sun.

The U.Mass. Sunwheel is a stone circle calendar which I created in 1997 on the campus of U.Mass. Amherst, with 8'-10' tall stones marking the cardinal directions, the solstice sunrise and sunset directions, and the northernmost and southernmost moonrise and moonset directions. Over 25,000 people have visited the Sunwheel since its construction, and over 10,000 have attended the seasonal sunrise and sunset gatherings which I host. The U.Mass. Sunwheel is one of the calendar sites around the world -- including Stonehenge, Callanish, and the "Sun Dagger" at Chaco Canyon -- where the 18.6-year cycle of the Moon is marked. The following material explains the monthly behavior of the Moon along with the 18.6-year lunar cycle, including why there is an 18.6-year cycle, and what the observable consequences of this cycle are. To understand the patterns in the movements of the Moon requires some familiarity with the somewhat simpler pattern in the movements of the Sun.

Explanation on patterns of the sun follows. Then here are the patterns for the moon:

• Where to find the Moon in the sky on any given day depends on 3 things:
  • (1) the phase of the Moon on that day
  • (2) where the Sun is in the sky
  • (3) where the Moon is in its 18.6 year cycle
  • Moon Phases:
• The Moon orbits, or revolves, around Earth and completes one revolution in 29.5 days. This is the same length of time that it takes the Moon to complete one cycle of phases. Becauseof the shorter period of revolution for the Moon around the Earth, compared to the revolution ofthe Earth around the Sun, the Moon completes between 12 and 13 cycles of lunar phases in 1 year.
  
  
• Thephases themselves arise because the light which lights the Moon is coming from the Sun, while our vantage point is the Earth. To understand the relative locations of the Sun and Moon in relation to the lunar phases, the simplest guides to remember are:
  • (1) the full Moon is opposite the Sun in the sky
  • (2) the new Moon is in the same direction as the Sun in the sky (and the side of the Moonwhich is illuminated by the Sun is the side we cannot see)
  • (3) the crescent Moon is always near the Sun in the sky
  [Contrary to popular misconception, the phases of the Moon do NOT arise from the Earth'sshadow. The only time the Earth's shadow falls on the Moon is during a totallunar eclipse.]
  Changing Direction of Moonrise and Moonset:
  The pattern in the Moon's movements is more complex than the Sun's for several reasons:
  
  • (1) The Moon completes one orbit around us in a much shorter time than 1 year (in 29.5 days orabout a month,in fact, in contrast to our orbit around the Sun with a period of 365.25 days).
    (2) The plane of the Moon's orbit is close to the plane of Earth's orbit around the Sun, butnot identical -- the Moon orbits us in a plane which is tilted by 5.1° relative to the ecliptic.
• Because of the rapid orbit of the Moon around us in a plane which is close to theplane in which we always see the Sun, THE MOON DOES IN A MONTH WHAT THE SUN DOES IN A YEAR, in terms of the changing rising and setting direction along the horizon. That is, themoonrise and moonset directions change like a pendulum, swinging back and forth along the horizon and completing one full swing each month. The Sun's pendulum-like swing continues much slower, with the Suncompleting one full swing each year.
  
  
• Because of the tilt of the Moon's orbital plane in relation to our orbit around the Sun, the outer extremes of the Moon's monthly range of rising and setting are NOT THE SAME as theouter extremes of the Sun's yearly range of rising and setting.
  
  
• Furthermore, the outer extremes of the Moon's monthly range of rising and setting arenot fixed, but change slightly from year to year with an 18.6-year cycle.

The moon's 18.6 cycle and why:

• THE MOON'S 18.6-YEAR CYCLE -- What and Why?
  
  
• The plane of the Moon's orbit is tilted at an angle of 5.1° to the plane of our orbit around the Sun.
  • This means that the Moon can at times be seen to rise and set more northerly and more southerly even than the solar extremes. [Recall that the changing sunrise and sunset direction every day is a result ofthe tilt of the plane in which we see the Sun in the sky in relation to the planethrough Earth's equator.]
• Due to the effects of the Sun's gravity, the Moon's orbital plane does not stay fixedin space, but "precesses" with an 18.6 year cycle, while still maintaining the 5.1° tiltrelative to the ecliptic.
  • This means that the most northerly and the most southerly rising and setting of the Moon occur every month at the peak of the 18.6 year cycle.
• The Moon's 18.6-year cycle peaks in 2006 and 2024-25 (and every 18.6 years thereafter), with observable consequences extending for at least 3 years around the peak year(s).
  • THE 18.6-YEAR LUNAR CYCLE IS OBSERVED AS A MODULATION IN THE OUTER EXTREMES OF THE MOON'S MONTHLY RANGE OF RISING AND SETTING.
    
    
  • MAJOR LUNAR STANDSTILL = maximum monthly range of Moon rising and setting
  • MINOR LUNAR STANDSTILL = minimum monthly range of Moon rising and setting(9.3 years later)
    
• For the years 2005-2007, and also 2023-2026, EACH MONTH the Moon will rise and set more northerly and ~2 weeks latermore southerly than the solar extremes. Also, EACH MONTH the Moon will transit higher in the sky than the summer Sun and ~2 weeks later lower than the winter Sun. This is the MAJOR LUNAR STANDSTILL. [The Moon's Declination (effectively the latitude on the sky) ranges each month between -28 and +28° .]
  
  • The following tables give the dates when the Moon will be at the northern and southernextremes during the years
    • 2005-2007
    • 2008-2010
    • 2011-2013
• 9.3 years after a major standstill, the monthly range of moonrise and moonset shrinks. Whatwe see is that each month the Moon will rise and set LESS northerly and ~2 weeks laterLESS southerly than the solar extremes. Also, EACH MONTH the Moon will transit NOT AS HIGH in the sky as the summer Sun and ~2 weeks later NOT AS LOW in the sky as the winter Sun. This is the MINOR LUNAR STANDSTILL.[The Moon's Declination (effectively the latitude on the sky) ranges each month between -18 and +18°.]
  The schematic diagram below shows the placement of the stones in the U.Mass. Sunwheel as seen from above, with large dots for the 8'-10' tall stones and the small dots for the 2'-4' tall stones. The Sunwheel includes stones for cardinal directions, solstices, and the northern and southern extremes of the lunar rising and setting seen at major standstill. The figure indicates the maximum monthly range of moonset and moonrise seen at major standstill, and the minimum monthly range of moonset and moonrise seen at minor standstill.

Why standstill?

• WHY THE TERM 'STANDSTILL' ?
  
  
• The monthly rangeof lunar Declination changes very little from 2005-2007 and also from 2023-2026. Also during this time, the monthly range of moonrise and moonset directions changes little. The fact of little change in the outer extremes of monthly range of rising and setting directions for ~3 years is what leads to the use of the term STANDSTILL.
  
  
• Solstice means 'STANDSTILL OF THE SUN' and refers to the fact that the Sun's Declination changes little for the ~2 weeks around solstice. The sunrise and sunset directions change little over this time as well.
  
  
• THE SUN'S ANNUAL CYCLE IN CHANGING SUNRISE DIRECTION BEHAVES LIKE A PENDULUM. The sunrise direction changes rapidly from day to day near the Equinox, like the rapid motion of a pendulum at mid-swing, and there is a stopping or 'standstill' at solstice, like the outer limit of the swing of a pendulum.
  
  
• Over the 18.6-year cycle of the Moon, THE CHANGING MOONRISE AND MOONSET DIRECTION BEHAVES LIKE A COMPOUND PENDULUM SYSTEM.
  • More time is spent monthly at the N and S extremes of moonrise and moonset than in the middle -- this behavior is described by the first pendulum.
    
    
  • And, from month to month within the 18.6-year cycle, the Moon spends more time with the monthly range of rising and setting at the outer extremes (major standstill) and at the inner extremes (minor standstill) than at the middle extremes.
    It is as if the pendulum representing the monthly range of lunar rising and setting is modulated by 2 additional small coupled pendulums, one at the Sun's northern risinglimit and one and the southern. When these 2 pendulums swing out we get MAJOR lunar standstill,and when they swing in we get MINOR lunar standstill.
• The fact that the Moon spends more time with the monthly range of rising and setting at the outer extremes (major standstill) and at the inner extremes (minor standstill) than at the middle extremes is the reason for the use of the term STANDSTILL.

Then follows descriptions of the major sites tracking this event: Stonehenge in England, Callanish in Scotland, Chaco Canyon in New Mexico, and the site that the professor above made at the University of Massachusetts.

This is what can be seen during a major lunar standstill:

At MAJOR STANDSTILL, the Moon exhibits the maximum monthly range of rising and setting directions.

• The full Moon near winter solstice in 2005-07 rises and sets the farthest North that the Moon ever gets, and farther north than the Sun ever gets. At transit, the winter solstice full Moon will be higher in the sky than the summer Sun ever gets. DID YOU NOTICE THIS around Dec. 27, 2004?
  
  
• The full Moon near summer solstice in 2005-07 rises and sets the farthest South that the Moon ever gets, and farther south than the Sun ever gets. At transit, the summer solstice full Moon will be lower than the winter Sun ever gets. [To notice this requires knowing which way South is, since a low Moon can also be one which is just rising or setting.] DID YOU SEE THIS at summer solstice 2005?
  
  
• The 1st and 3rd quarter Moons around equinox during 2005-2007 are at the northern and southern extremes of the Moon rising and setting. In particular, around the spring equinox in 2005, we hadhigh Moon on March 18, and a low Moon 2 weeks later on April 1-2.
  
  
• The crescent Moon near winter solstice will be the southern rising and setting Moon (see diagrambelow). The crescent Moon near summer solstice will be the northern rising and setting Moon.
  
  
  
  

The following table lists the dates, phases, and declinations for the Moon at the southernmost and northernmost extremes for each month during the period 2005-2007, centered on the year 2006 when the Moon is at the peak of its 18.6-year cycle. These data were derived using the 'Ephemeris Generator' available through JPL:

DATES of LUNAR EXTREMES during the 2005-2007 MAJOR LUNAR STANDSTILL

Sunwheel - Proposed and constructed under the watchful eye of Professor Judith Young of the Astronomy Department at the University of Massachusetts in Amherst

www.umass.edu

 

[Gaby]

I like this article because it is more basic for beginners:

Major Lunar Standstill

Major Lunar Standstill occurs every 18.6 years when the moon reaches a maximum monthly range of moonrise/set to the north and south. This range is beyond the range that the sun reaches at...

www.exploreglobe.net

Major Lunar Standstill occurs every 18.6 years when the moon reaches a maximum monthly range of moonrise/set to the north and south. This range is beyond the range that the sun reaches at solstices. During Major Standstills the lunar nodes are oriented in line with the equinoxes and the high point in the lunar orbit is aligned with the direction of Northern Solstice and the low point with the direction of Southern Solstice to produce an additive effect to achieve maximum declinations to the north and south of the ecliptic. During Major Lunar Standstill eclipses occur near Equinoxes. Since the cycle takes 18.6 years to complete, there are limited opportunities to make direct observations and to document maximum lunar positions at the myriad sites that have possible connections that still exist to any extent. For many ancient sites with putative precision alignments, actual observation, while intriguing, is of limited use because the extreme positions of the sun or moon at the time the alignments were created are no longer attained due to the decreasing obliquity of Earth's orbit over the last few thousand years. However, for general alignments to ancient maximum rising/setting events, positions can be calculated easily from observations near modern maximums.

The next Major Lunar Standstill is in 2025, but the 18.6 year cycle of the moon moves it through a range of maximum declination values that are often measured geocentrically (from the center of the Earth) but for practical observation purposes the moon might not be in the sky at the absolute maximum value for any observer, and even if it is in the sky at that moment, viewer latitude changes the angle at which the moon is seen (parallax) and so that particular date might not be the most extreme position viewable for a particular location. There are other orbital mechanics at play as well. What it really comes down to for observing from a particular location is that the moon already reaches very close to maximum rising/setting positions on the horizon at the end of 2023 and for all of 2024 and 2025 and even into some of 2026. For all of that time it will reach extreme positions every month at various phases and with slight fluctuations (see chart below). The absolute extreme positions are attained near half moons around March and September. The absolute maximum geocentric declination will be March 2025, but again latitude can affect how this looks observationally. Also with that range of years it sounds like a lot of opportunities for viewing, but with some phases hard to observe in daylight and with any cloud interference, the possibilities are reduced. For observation/viewing purposes it ideal to take advantage of every opportunity over these years when conditions are right.

Possible Major Sites for Initial Documentation:

Thornborough Henges
Tirghoil standing stone
Gaoutabry Dolmen
Chûn Quoit
Drift Stones
La Pierre Droite (Peyrolles)
Beaghmore
Ballynoe

It looks like September 1st or 14th are good candidates:

Here is an Excel sheet with more details:

Major Lunar Standstill

Major Lunar Standstill DATES Please Support the Work <a href="http://facebook.com/groups/archastrodb">Facebook</a> Major Lunar Standstill,<a href="https://www.youtube.com/ArchaeoastronomyDatabase">YouTube</a>,Current Date and Time (UTC),Standstill Event / Date Selection <a href="https://www.exp...

docs.google.com

 

[Gaby]

Here is some data of the 2006 event:

Lunar standstill - Wikipedia

en.wikipedia.org

Geniet: Investigating the major standstills limit event in 2006

And ongoing research for 2024/2025:

Geniet: Investigating the major standstill limit event in 2024/2025

 

[BlueKiwi]

I saw the moon take on a weird trajectory two nights ago. I'm outside every hour or so, smoking, so I observe the moon whenever it's out. From where I am in New Zealand, this is it's normal path :




And this was it's path two night ago :



Well, I mentioned this to my wife, and she thinks I'm nuts. Sorry in advance about the bad drawings. I'm not sure if this qualifies as a lunar standstill, but in any case, I've never seen it so anything like this, and I've been smoking at night outside for about 30 years.

 

[Gaby]

It's that time of the cycle!

The 1st 'major lunar standstill' in more than 18 years is about to occur. Here's how to see it.​

The 1st 'major lunar standstill' in more than 18 years is about to occur. Here's how to see it.

A major lunar standstill is about to occur. The phenomenon happens every 18.6 years when the moon rises and sets at its most extreme points on the horizon, while also climbing to its highest and lowest point in the sky.

www.livescience.com

A major lunar standstill is about to occur. The phenomenon happens every 18.6 years when the moon rises and sets at its most extreme points on the horizon, while also climbing to its highest and lowest point in the sky.
In addition to the April 8 total solar eclipse and vibrant displays of auroras, there's another celestial treat for skywatchers this year: the first "major lunar standstill" since 2006. During this event, the moon rises and sets at its most extreme northerly and southerly positions on the horizon, reaching its highest and lowest points in the 18.6-year lunar cycle.

This is possible because the moon doesn't follow the same path as the sun. Its rising and setting positions on the horizon change constantly due to the movements of Earth and the moon. The solar system is flat, with the planets orbiting the sun on the same plane, known as the ecliptic. Earth rotates on an axis tilted by 23.4 degrees with respect to this ecliptic, causing the sun to rise and set within almost 47 degrees — a range it gradually covers over an entire year. The moon's orbit is tilted by 5.1 degrees relative to the ecliptic, allowing it to rise and set within a 57-degree range in any given month.

This explains why the moon can sometimes rise and set at points on the horizon farther north and south than the sun can.

A major lunar standstill, or lunistice, occurs when the tilts of both Earth and the moon are at their maximum. During this period, the moon rises and sets at the extremes of its range. It rises at its very highest northeasterly point and sets at its very highest northwesterly point. During this period, it also rises at its most southeasterly point and sets at its most southwesterly point.

The major lunar standstill significantly affects how long the moon is in the sky at night. A moon rising farthest northeast in the Northern Hemisphere climbs higher into the sky and stays in the sky longer. It shines in a noticeably different position than during a minor lunar standstill, when the range of where it rises and sets is at its narrowest. Historical sites such as Stonehenge, Callanish and Newgrange appear to be aligned with moonrise and moonset points during a major lunar standstill, indicating the celestial event’s past importance.

This major lunar standstill will be at its most extreme around the equinoxes in September 2024 and March 2025. However, visibility depends on the moon's phase, your location and the weather. Good times to look include when the moon rises and the sun sets, and vice versa, during a full moon.

On June 21, the sun will rise and set at its most northeasterly and northwesterly points, while the full Strawberry Moon will rise and set at its most northeasterly and northwesterly points. Conversely, on Dec. 15, the sun will rise and set at its most southeasterly and southwesterly points, while the full Cold Moon will rise and set at its most northwesterly and northeasterly points.

To observe these phenomena, watch from exactly the same location, and you'll notice a big difference. A pair of stargazing binoculars or a good backyard telescope aren't necessary to notice the effect, but they may help you zoom in on Earth's fully-illuminated satellite to get the most out of your lunar skywatching.

 

[ScioAgapeOmnis]

Historical sites such as Stonehenge, Callanish and Newgrange appear to be aligned with moonrise and moonset points during a major lunar standstill, indicating the celestial event’s past importance.

And Stonehenge has just been vandalized by anti-oil whackos. Given the above, the timing is a bit curious:

Stonehenge sprayed with orange powder paint by Just Stop Oil activists

Two people arrested, say police, while Rishi Sunak’s comments on protest prompt response from Labour donor

www.theguardian.com

 

[Benjamin]

Maybe this was already brought up somewhere (apologies), but while combing the transcripts for many something elses, I saw in this section from Sept. 25, 1999 a discussion about the tetrahedron in a sphere, spheres being windows and portals, Hoagland, and the 19.5 and 18 degree references. I thought it was a bit odd that the degree numbers were similar to the 19 year cycle happening every 18.6 years.

Q: There could be many explanations. Now, we have a correspondent who wrote and asked a question. He said that he noticed there was promotion of Hoagland's idea about the 19.5 degree tetrahedral configuration at one point, and then another idea regarding the parallelogram business involving an 18 degree mark in another section. So, what is the difference between the 19.5 degree comments of Hoagland, and the 18 degree point of interest that you brought up? Are we talking about two different things here?

A: Well, if you do the math, you see that 18 degrees fits nicely with ninety. Maybe 19.5 is due to crustal slippages in some"land mark" event?!

Q: (A) But, in geometry, this 19.5 degrees is what you get when you try to put a tetrahedron into a sphere. That's how Hoagland got it, not because of observation.

A: Okay, that is good, too.

Q: How come you didn't know that?

A: We pointed it out in the first place.

Q: Is that why you put "landmark" in quotes? That 19.5 is where it touches. It is the mark of the point of contact. Is that it?

A: Clues, my dear, clues, and the eternal need not to abridge free will.

Q: But, if these tetrahedrons fit in a sphere, and they touch the sphere at 19.5 degrees, how do they relate to this effect that you have said manifests at 18 degrees?

A: Does 1.5 fit into 90? Does 90 fit into 180? Does 180 fit into 360? Ask yourself, "what does it mean?"

Q: We don't know. (A) The point is that the angle Hoagland is talking about is not 19.5, it is an approximation of point something, something, something.... So, if it is just 19.5, that's the difference between 19.5 and 18 - that is 1.5, which, in this case, is not exactly 1.5, it's one point something which does not fit into anything that we know.

A: Circumference.

Q: (A) Yes. 360 degrees. Is the circumference important?

A: It is important.

Q: (A) So, we can compute these two circumferences, and these will differ by some number, and this number will fit again into one of these circumferences, and the point is that it sould fit so that there is an integer number...

A: Yes.

Q: (A) But, there will then be many more angles. There will be not only 18 and 19.5...

A: Yes. All Hoagland has done is highlight a point at which magnetic lines converge using the tetrahedron model.

Q: If they converge at that point...

A: But the question is how does the tetrahedron model relate to trans-dimensional space?

Q: How does the tetrahedron model relate to trans-dimensional space?

A: A key which unlocks the door.

Q: Speaking of a key that unlocks a door: there is some information going around that a gigantic computer has been installed inside the earth that was put there by a Reptilian race, and that the recovery of this thing is one of the reasons for the current or upcoming "invasion" by them. Does this tetrahedron configuration in the earth relate to some giant alien computer?

A: No.

Q: Is there a giant alien computer buried in the Earth?

A: Not likely that.

Q: Back to the tetrahedron. How is it a key to trans-dimensional space? Does one activate it in some way? Do you place machinery of some sort at these points?

A: No. Magnetism.

Q: Are you supposed to generate magnetism, or is it natural magnetism?

A: Natural.

Q: Are you supposed to do anything to it or with it?

A: Supposed???

Q: Is it useful to do something with it?

A: Can be.

Q: In what sense?

A: Travelling between dimensions.

Q: Is anybody at the present time utilizing it in this way?

A: Not terran STS 3rd density.

Q: That implies that 4th density STS IS doing this. Could one construct a scale model of a tetrahedron in a sphere, magnetize it, and open portals?

A: Yes.

Q: Would it require a lot of electrical current?

A: Yes.

Q: Is there anyway to travel between dimensions, in space time, or whatever, utilizing very little power, as such?

A: Off the point we told you before that all spheres of cosmic nature are windows.