You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Interesting videos about science
- Thread starter Pierre
- Start date
Resembles an electric lightning bolt

This is amazing! This a shot from the surface of Mars taken by NASA’s Curiosity Rover. It will be amazing to see what their Perseverance Rover that landed last week will be able to capture. | This is amazing! This a shot from the surface of Mar
15 Mio. views, 199.339 likes, 8.930 loves, 33.923 comments, 37.001 shares, Facebook Watch Videos from Alan Tudge MP: This is amazing! This a shot from the surface of Mars taken by NASA’s Curiosity...
 fb.watch
fb.watch
"Here's a philosophical question for you. If a color doesn't have a name, can we still see it? Many years ago, the human eye evolved to give us the ability to see about a million colors. That's a lot. Then how come, until very recently, nobody saw or even heard of the color blue? Well, it's because blue just -- didn't exist yet. Let's find out why. "
EricLux
Dagobah Resident
Looks like stereographic projection thanks to the light

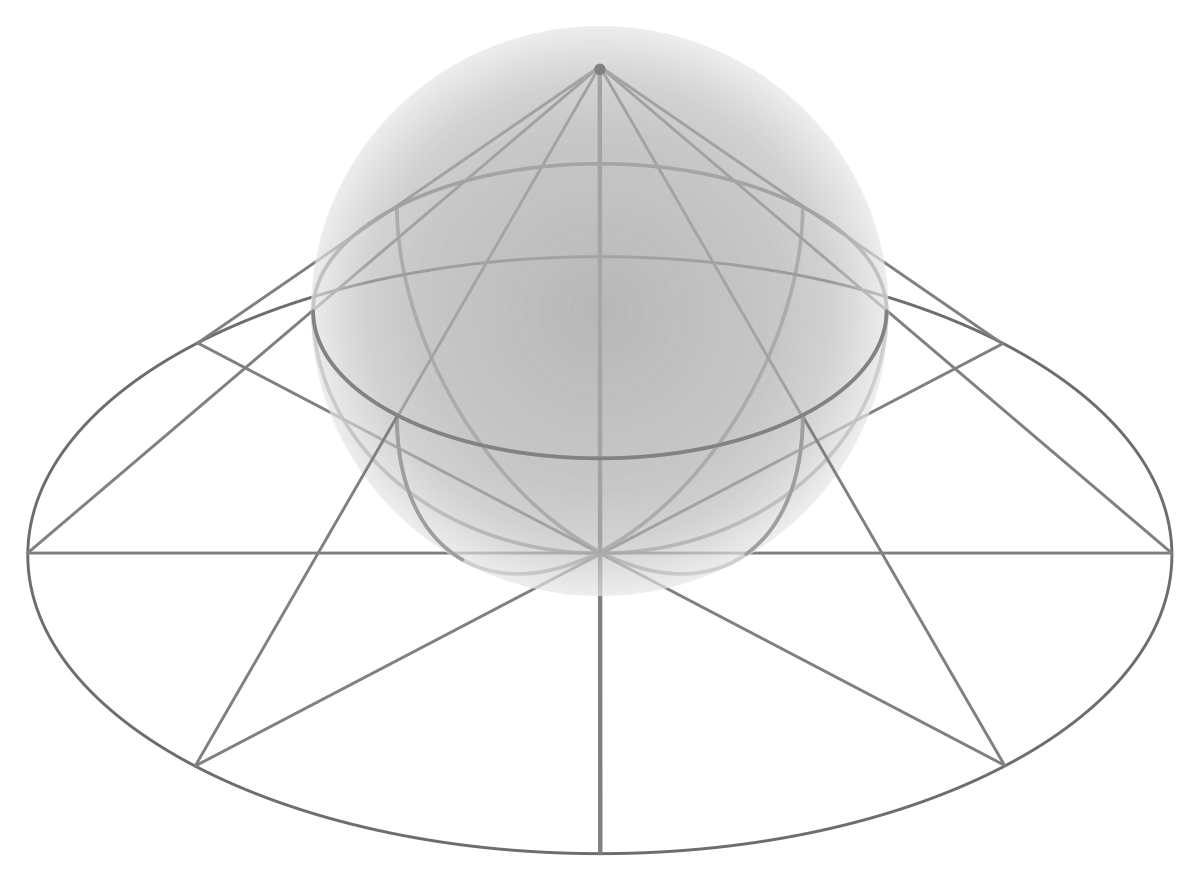
Stereographic projection - Wikipedia
PabloAngello
Jedi Master
"Pyrex has exactly the same refractive index as vegetable oil. Thus, a Pyrex object becomes perfectly invisible when it is immersed in oil. Fascinating to watch!"
EricLux
Dagobah Resident
It's really amazing ! You realize if there were realities with the same refractive index as air. Finally, so many "dimensions" or realities around us that we are not even aware of"Pyrex has exactly the same refractive index as vegetable oil. Thus, a Pyrex object becomes perfectly invisible when it is immersed in oil. Fascinating to watch!"

Merci @Pierre ! One more thing about the vibration of light !
EricLux
Dagobah Resident
"Pyrex has exactly the same refractive index as vegetable oil. Thus, a Pyrex object becomes perfectly invisible when it is immersed in oil. Fascinating to watch!"
After the fact that π is different in circular motion compared to linear motion than what we observe in outer physics and math, there is the Cherenkov effect produced by speeds greater than c/n the speed of light relative to water with a refractive index n different from that of air. What if the blue color of the terrestrial sphere reflected speeds greater than c, the speed of light in the air?
In other words, what if the atmosphere at high altitude had a lighter density than the air, since it was more rarefied, with a refractive index less than 1 and therefore a superluminal speed? This would mean that the measurement c that we attribute to light would only be valid locally, at the terrestrial level and that we would have extended our theoretical hypothesis, based on terrestrial observation, to the whole universe... mmm... we are entitled to ask if we wouldn't have there part of the explanation of the particular dynamics of the Pioneer probes in the solar system... mmm... but then space, the speed of light would be relative, related to the distribution of matter and antimatter, the matter-antimatter matrix ? And as the C's mentioned, all this would be linked to a difference in gravity.
We would find there the fact that the speed of light is linked to gravity, the EM density of the medium in question as the C's said, in the last session, in response to @Pierre's questions on the speed of light.
In other words, what if the atmosphere at high altitude had a lighter density than the air, since it was more rarefied, with a refractive index less than 1 and therefore a superluminal speed? This would mean that the measurement c that we attribute to light would only be valid locally, at the terrestrial level and that we would have extended our theoretical hypothesis, based on terrestrial observation, to the whole universe... mmm... we are entitled to ask if we wouldn't have there part of the explanation of the particular dynamics of the Pioneer probes in the solar system... mmm... but then space, the speed of light would be relative, related to the distribution of matter and antimatter, the matter-antimatter matrix ? And as the C's mentioned, all this would be linked to a difference in gravity.
We would find there the fact that the speed of light is linked to gravity, the EM density of the medium in question as the C's said, in the last session, in response to @Pierre's questions on the speed of light.
christx11
Jedi Master
What do you think about this? I'm wondering what C's would say about it
I may be mistaken, but from my perspective this has nothing to do with pi. It is about forces. Both balls initially are dealing with 2 forces, gravity and friction. When the ball goes into the loop it is now dealing with an additional force created by the loop, if there was not this additional force the ball would go straight, like the other one. It doesn't. That additional force is what is causing the perceived difference. It has nothing to do with pi. That additional force actually makes the ball in the loop move ever so slightly slower. The experiment is about forces, not pi.
EricLux
Dagobah Resident
I may be mistaken, but from my perspective this has nothing to do with pi. It is about forces. Both balls initially are dealing with 2 forces, gravity and friction. When the ball goes into the loop it is now dealing with an additional force created by the loop, if there was not this additional force the ball would go straight, like the other one. It doesn't. That additional force is what is causing the perceived difference. It has nothing to do with pi. That additional force actually makes the ball in the loop move ever so slightly slower. The experiment is about forces, not pi.
Exactly ! Thanks for your answer Chris. And this is where it gets interesting: whereas, in static 3D mathematics, when we relate circular to linear, when we measure circular in a linear way, we introduce the concept π as a conversion constant. When we leave the field of pure mathematics, we are entitled to ask ourselves what distinguishes math from physics by verifying whether, in the field of dynamics, the externally and theoretically observed value of π is always the same.
Let's not forget that when we pass from kinematics to dynamics, in Einstein relativity, π already varies for extremely high speeds. And as we describe the circular, starting from the linear, through π, wouldn't π finally describe the relation of forces between the linear and the circular? The question is entitled to ask when we remember that the C's told us that in 4D, we perceive the inside and the outisde, at the same time, thanks to the 4th "dimension" that Einstein identified with linear time, for linear and non-circular movements.
Instead of having to reach speeds close to the speed of light to observe a different π, in linear speed, we could obtain the same result by difference of a linear speed and a circular speed? In other words, could an observed difference between linear velocity and acceleration result in a different π? Interestingly, you talk about additional force, where the C's talk about an additional spatial reference to better understand reality.
Even more surprisingly, we can observe elements that go in the same direction with the cycloid. What if instead of adding a force, we could modify our mathematical constants? In any case, there is only experience to settle the debate.
Let's not forget that when we pass from kinematics to dynamics, in Einstein relativity, π already varies for extremely high speeds. And as we describe the circular, starting from the linear, through π, wouldn't π finally describe the relation of forces between the linear and the circular? The question is entitled to ask when we remember that the C's told us that in 4D, we perceive the inside and the outisde, at the same time, thanks to the 4th "dimension" that Einstein identified with linear time, for linear and non-circular movements.
Instead of having to reach speeds close to the speed of light to observe a different π, in linear speed, we could obtain the same result by difference of a linear speed and a circular speed? In other words, could an observed difference between linear velocity and acceleration result in a different π? Interestingly, you talk about additional force, where the C's talk about an additional spatial reference to better understand reality.
Even more surprisingly, we can observe elements that go in the same direction with the cycloid. What if instead of adding a force, we could modify our mathematical constants? In any case, there is only experience to settle the debate.

