John G
The Living Force
Very loosely as far as I saw from the first link, because we're talking about using Pythagorean triples as a roadmap for progression in/to building our dimensional set of existence, and that our 3 spatial dimensions (Front/Back, Left/Right and Above/Below) seem to stem from intersection of primarily two planes of existence, two planes orthogonal to Inner/Outer direction of a particular dimension of existence, something like a field of angular distances WRT field of radial ones.
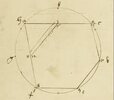
Regarding Pythagorean triples (a, b, c), where c^2 = a^2 +b^2, when we check primitive ones with numbers up to 300, 6 patterns of triples of sequences emerge:
Like the Cs said (paraphrasing): "Geometry will get you there, but you need algebra to get around".
- 3 'basis' triples:
- already shown (2n+1, 2n(n+1), 2(n + (1+I)/2)(n + (1-I)/2)) - from primitive triples like (3,4,5), (5,12,13), (7,24,25), ..., where for n=0 we get (1, 0, 1) and for n<0 again valid primitive triples just with some of the number being integers besides ordinary naturals;
- (4(n+1), (2n+1)(2n+3), (2(n+1) + I)(2(n+1) - I)) - from triples like (8, 15, 17), (12, 35, 37), (16, 63, 65), ..., where for n=0 we get (4, 3, 5) and for n=-1 (0, -1, 1);
- (4(2n+3), (2n+1)(2n+5), ((2n+3) + 2I)((2n+3) - 2I)) - from triple like (20, 21 29), (28, 45, 53), (36, 77, 85), ..., where for n=0 we get (12, 5, 13);
- 3 triples of sequences of 'higher/lower' order which use above 3 triples for the sort of basis and also some of their elements as part of their own sequences:
- (3(2n+9), (2n+6)(n+6), 2(n + (9+3I)/2)(n + (9-3I)/2)) - where for n=0 we get (27, 36, 45) = 3^2 * (3, 4, 5) and on places of 3rd, 6th, 9th, ..., elements in the sequence stand respectively 3^2*2nd, 3^2*3rd, 3^2*4th, ..., elements from sequence 1 above;
- (12(n+3), (2n+3)(2n+9), ((2n+6) + 3I)((2n+6) - 3I)) - where for n=0 we get 3^2 * (4, 3, 5) and on places of 3rd, 6th, 9th, ..., elements in the sequence stand respectively 3^2*1st, 3^2*2nd, 3^2*3rd, ..., elements from sequence 2 above;
- an interesting (5(2n+11), (2n+6)(n+8), (2(n + (11+5I)/2)(n + (11-5I)/2))) - where for n=0 we get (55, 48, 73) which is permuted 1st element of previous sequence 2 here and where on place of 2nd element in the sequence we have 5^2 * (3, 4, 5), while for n=-3 we get (25, 0, 25).
In above post and that thread, proposed approach is to treat gravity and e-m like two 'effects' of the same thing - gravity as radial component, difference/distance from non-existence in the direction of a particular dimension of existence, and e-m as angular plane (of angular distances/differences) orthogonal to that direction - which would basically incorporate all directions/dimensions of existence available to that particular one, with that particular one being in the 'center' of that plane of angular distances.
Well this version does get our 3-dim space via a boundary of 4-dim one with the extra an in-out one of sorts and it can do triangle reflections but yes there's differences. The 4th dimension is supposed to do the can't tell left from right and pentagons look like triangles kind of thing and I think there's some kind of reflection thing that goes with that.
The triangle A'B'C' is a translation of triangle ABC, with the translation being produced by two reflections by two of the parallel lines in the pencil of parallel lines from the given boundary point.
The horocycles at the given boundary point are the paths of parabolic translation isometries of the Unit Disk generated by reflections by the parallel lines in the pencil of parallel lines from the given boundary point...
This link also mentions Ark a few times and the math Ark uses for gravity gets mentioned:
The SO(4,2) would be Ark's gravity, the 4+2=6 being the hexagon the Cs mention a few times and the Cs confirmed the 4 and 2 also. EM would be an SO(2), unfortunately not the SO(2) mentioned in this link. Mixing gravity (gravitons) and EM (photons) is less simple than looking at them on their own and there are spacetime (metric, volume form, structure group, etc.) messes too for both of them.Type IV(4) domains have been used to understand physics by Coquereaux and Jadczyk. An example of their line of thinking is given by the following quote from the paper by R. Coquereaux entitled Lie Balls and Relativistic Quantum Fields, Nuc. Phys. B. 18B (1990) 48-52:
"... In the present paper, we are mainly interested in the four dimensional (complex) Lie ball that we shall denote by D. This smooth manifold can be written as SOo(4,2) / SO(4)xSO(2) or as SU(2,2) / S(U(2)xU(2)). ... D is a bounded non compact symmetric domain of type I and IV. ... The metric of D is euclidean and blows up near the boundary (as in the usual geometry of Lobachevski) but ... induces a conformal Lorentz structure on the boundary. The domain D is a Lie ball ... the Shilov boundary (compactified Minkowski Space-Time) can be defined as the Lie sphere ... The domain D also admits an unbounded realization: the future tube. ... This last unbounded realization of the Lie ball admits a simple physical interpretation. ... the imaginary part y of z = x + iy can be interpreted as the inverse of a momentum ... Points of the domain D describe therefore both the position (in space and time) and the momentum (with p^2 > 0) associated with a physical event. The domain itself becomes therefore a curved relativistic phase-space. Interpretation of Im(z) as an inverse momentum is an obvious four-dimensional generalization of what is done in usual wavelet analyisis (where the variable v in z = t + i/v is interpreted as a frequency). ...".
Two other papers with similar approach are:
CONFORMAL THEORIES, CURVED PHASE SPACES, RELATIVISTIC WAVELETS AND THE GEOMETRY OF COMPLEX DOMAINS, by R. COQUEREAUX and A. JADCZYK Received 28 December 1989, Revised 24 April 1990 Reviews in Mathematical Physics, Volume 2, No 1 (1990) 1-44
and
BORN'S RECIPROCITY IN THE CONFORMAL DOMAIN, by ARKADIUSZ JADCZYK, in Z. Oziewicz et al. (eds.) Spinors, Twistors, Clifford Algebras and Quantum Deformations, 129-140. (Kluwer Academic Publishers 1993)